filmov
tv
solve differential equation with substitution

Показать описание
solve differential equation with substitution,
blackpenredpen
blackpenredpen
solve differential equation with substitution
Differential Equations - Substitution Type (1) : ExamSolutions Maths Tutorials
How to solve differential equations by substitution
Solve second order differential equation by substitution, Q10 on review sheet
The Bernoulli Equation // Substitutions in Differential Equations
Substitutions for Homogeneous First Order Differential Equations (Differential Equations 20)
solve differential equation with substitution
Differential Equations: Solutions by Substitution
live lec-8 integration by substitution method calculus
Solving Differential Equations by Substitution
Solve a differential equation by substitution, v=x^3+y^3, an exam question
Solving the Differential Equation dy/dx = (x + y + 6)^2 with a Substitution
Homogeneous Differential Equations
Solving Differential Equations with a Composition (Obvious) Substitution (Differential Equations 22)
Solve a differential equation by substitution: dy/dx=(x-y+5)^2 (answer on WolframAlpha)
Solving a First Order ODE by Substitution An Example
Homogenous differential equation by substitution
Solve Differential Equation with substitution in urdu / Differential Equation /Zahra lectures
Solve a differential equation by substitution: dy/dx=(x-y+5)^2
How to Solve differential equations by using appropriate substitution.
Solving Differential Equations with Embedded Derivative Substitutions (Differential Equations 24)
§4.2 Solving A Differential Equation Using U Substitution (#49-50)
Separable First Order Differential Equations - Basic Introduction
How to solve adifferential equation with u=y/x substitution
Комментарии
 0:05:36
0:05:36
 0:11:32
0:11:32
 0:08:15
0:08:15
 0:07:47
0:07:47
 0:09:19
0:09:19
 1:05:45
1:05:45
 0:04:56
0:04:56
 0:27:12
0:27:12
 1:09:07
1:09:07
 0:08:01
0:08:01
 0:06:04
0:06:04
 0:05:29
0:05:29
 0:26:55
0:26:55
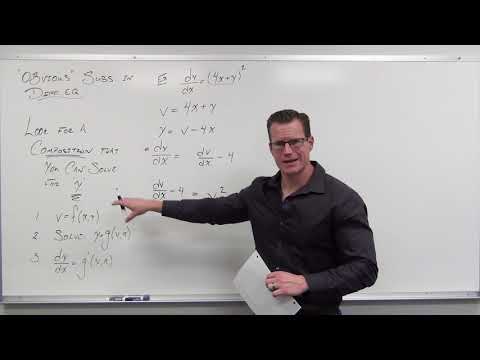 0:40:03
0:40:03
 0:19:13
0:19:13
 0:03:05
0:03:05
 0:07:21
0:07:21
 0:16:11
0:16:11
 0:15:32
0:15:32
 0:06:34
0:06:34
 0:47:31
0:47:31
 0:04:07
0:04:07
 0:10:42
0:10:42
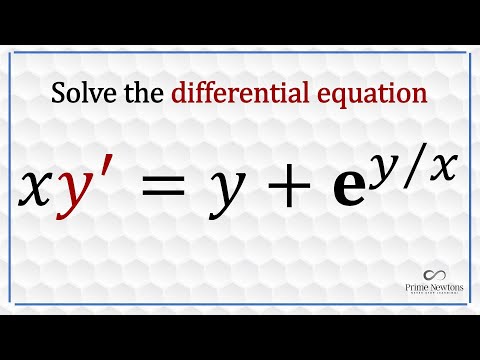 0:08:33
0:08:33