filmov
tv
Number Theory | When does a linear congruence have a solution??

Показать описание
We give the proof of a proposition regarding linear congruences and their solvability.
The Most Efficient Way for Beginners to Start Understanding Number Theory!
Number Theory | Divisibility Basics
What does a ≡ b (mod n) mean? Basic Modular Arithmetic, Congruence
Number Theory | When does a linear congruence have a solution??
Mathematicians Use Numbers Differently From The Rest of Us
Algebraic number theory - an illustrated guide | Is 5 a prime number?
Philosophy of Numbers - Numberphile
How to Learn Number Theory
Euclidean Algorithm - An example ← Number Theory
Number Theory | Linear Congruence Example 2
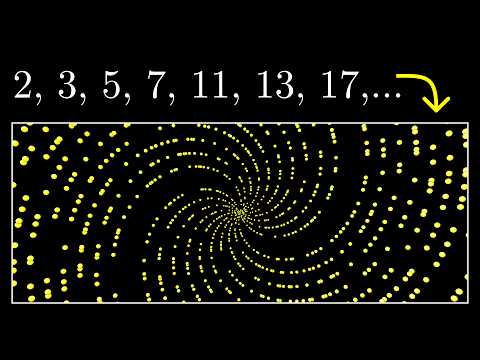
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
The High Schooler Who Solved a Prime Number Theorem
Number Theory: The Euclidean Algorithm Proof
The Mathematics of Cryptography
Number Theory Divisibility Proof
What does it feel like to invent math?
A number theory proof
Number Theory: Queen of Mathematics
The hidden link between Prime Numbers and Euler's Number
The Math Needed for Computer Science (Part 2) | Number Theory and Cryptography
Is math discovered or invented? - Jeff Dekofsky
An awesome number theory contest problem
Number Theory: The Division Algorithm
A throwback number theory problem
Комментарии
 0:02:29
0:02:29
 0:07:13
0:07:13
 0:05:45
0:05:45
 0:11:01
0:11:01
 0:33:06
0:33:06
 0:20:31
0:20:31
 0:09:41
0:09:41
 0:02:59
0:02:59
 0:02:04
0:02:04
 0:04:44
0:04:44
 0:22:21
0:22:21
 0:05:15
0:05:15
 0:05:50
0:05:50
 0:13:03
0:13:03
 0:03:37
0:03:37
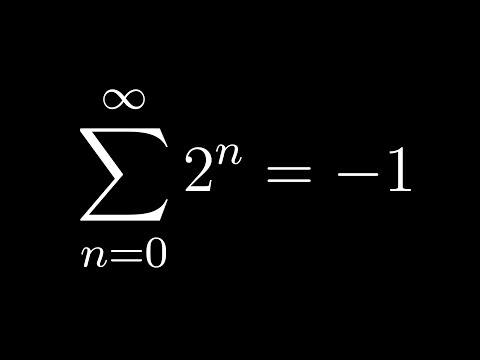 0:15:08
0:15:08
 0:10:17
0:10:17
 1:02:35
1:02:35
 0:12:29
0:12:29
 0:08:08
0:08:08
 0:05:11
0:05:11
 0:14:16
0:14:16
 0:12:49
0:12:49
 0:11:13
0:11:13