filmov
tv
What does it feel like to invent math?
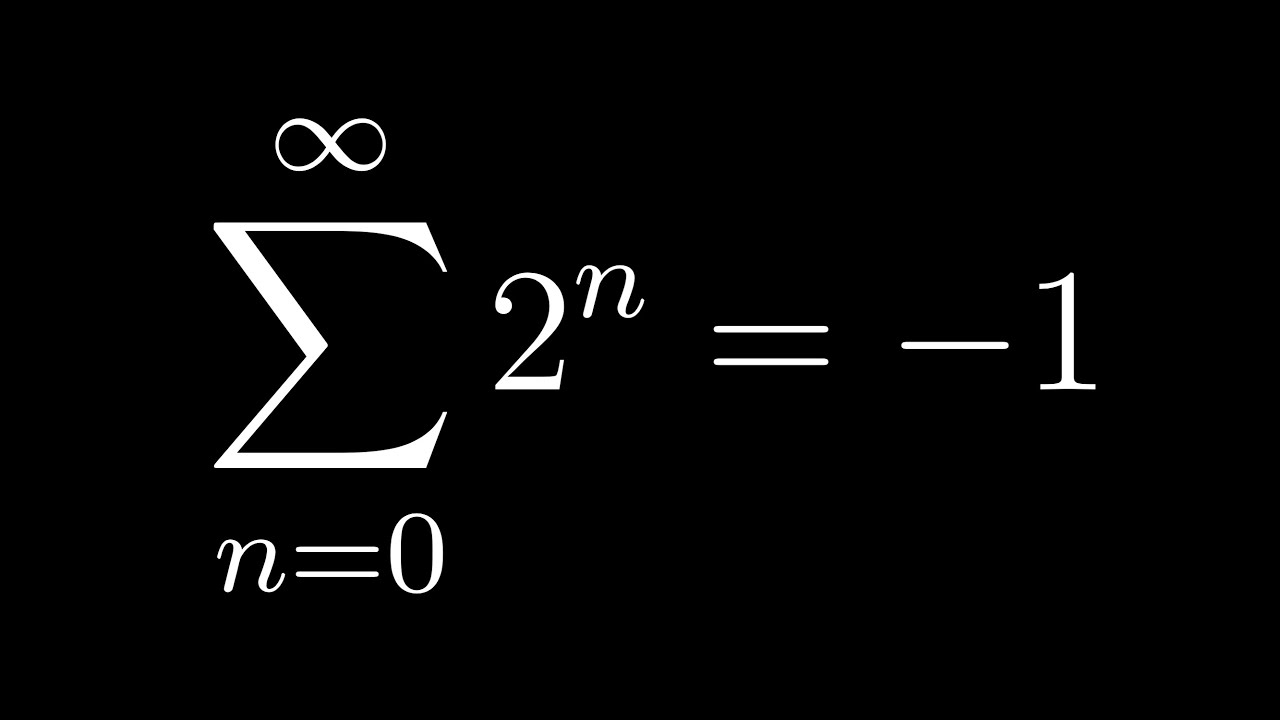
Показать описание
An exploration of infinite sums, from convergent to divergent, including a brief introduction to the 2-adic metric, all themed on that cycle between discovery and invention in math.
Music: Legions (Reverie) by Zoe Keating
Thanks to these viewers for their contributions to translations
Italian: Marco Fantozzi
Thai: @korakot, own doggoV●ᴥ●V
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
Music: Legions (Reverie) by Zoe Keating
Thanks to these viewers for their contributions to translations
Italian: Marco Fantozzi
Thai: @korakot, own doggoV●ᴥ●V
------------------
3blue1brown is a channel about animating math, in all senses of the word animate. And you know the drill with YouTube, if you want to stay posted about new videos, subscribe, and click the bell to receive notifications (if you're into that).
Various social media stuffs:
#LetsTalkAboutIt: What Does Anxiety Feel Like?
It's way different than you think
What Does Anxiety Feel Like?
What Does an Arrhythmia Feel Like?
Epilepsy. What does it feel like to have a seizure?
Armin van Buuren feat. Trevor Guthrie - This Is What It Feels Like (Official Music Video)
What Does It Feel Like? (Röyksopp Return the Sun Mix)
What does having a heart attack feel like?
What Does it Feel Like (Royksopp Return To The Sun Remix)
What Does it Feel Like to Have Autism? | Autism Awareness | Operation Ouch | Nugget
What Does Anxiety Feel Like?
Armin van Buuren feat. Trevor Guthrie - This Is What It Feels Like (Live at The Best Of Armin Only)
What does anxiety feel like?
What does a stroke feel like? - Prof. Michael Brainin - WSC 2022
Chest pain & angina: what does it feel like and what causes it?
What Does Dissociation Feel Like?
What does high blood pressure feel like?
What does radiation feel like?
But what does Masking feel like from the Inside?
What Does an ACL Tear Feel Like? With Dr. Bill Sterett, Orthopaedic Surgeon
Diabetes hypos | What does hypoglycaemia Feel Like? | Diabetes UK
What does it feel like when you have a torn rotator cuff?
What Does Autism Feel Like (Part One) - Go Inside My Autistic Mind
What Does a Meniscus Tear Feel Like? With Dr. Bill Sterett, Orthopaedic Surgeon
Комментарии
 0:09:26
0:09:26
 0:05:03
0:05:03
 0:01:02
0:01:02
 0:00:43
0:00:43
 0:04:21
0:04:21
 0:04:10
0:04:10
 0:05:48
0:05:48
 0:04:25
0:04:25
 0:07:13
0:07:13
 0:04:21
0:04:21
 0:01:03
0:01:03
 0:06:55
0:06:55
 0:00:59
0:00:59
 0:01:14
0:01:14
 0:06:17
0:06:17
 0:07:31
0:07:31
 0:03:10
0:03:10
 0:00:37
0:00:37
 0:18:27
0:18:27
 0:00:34
0:00:34
 0:01:16
0:01:16
 0:01:21
0:01:21
 0:11:50
0:11:50
 0:00:33
0:00:33