filmov
tv
A throwback number theory problem
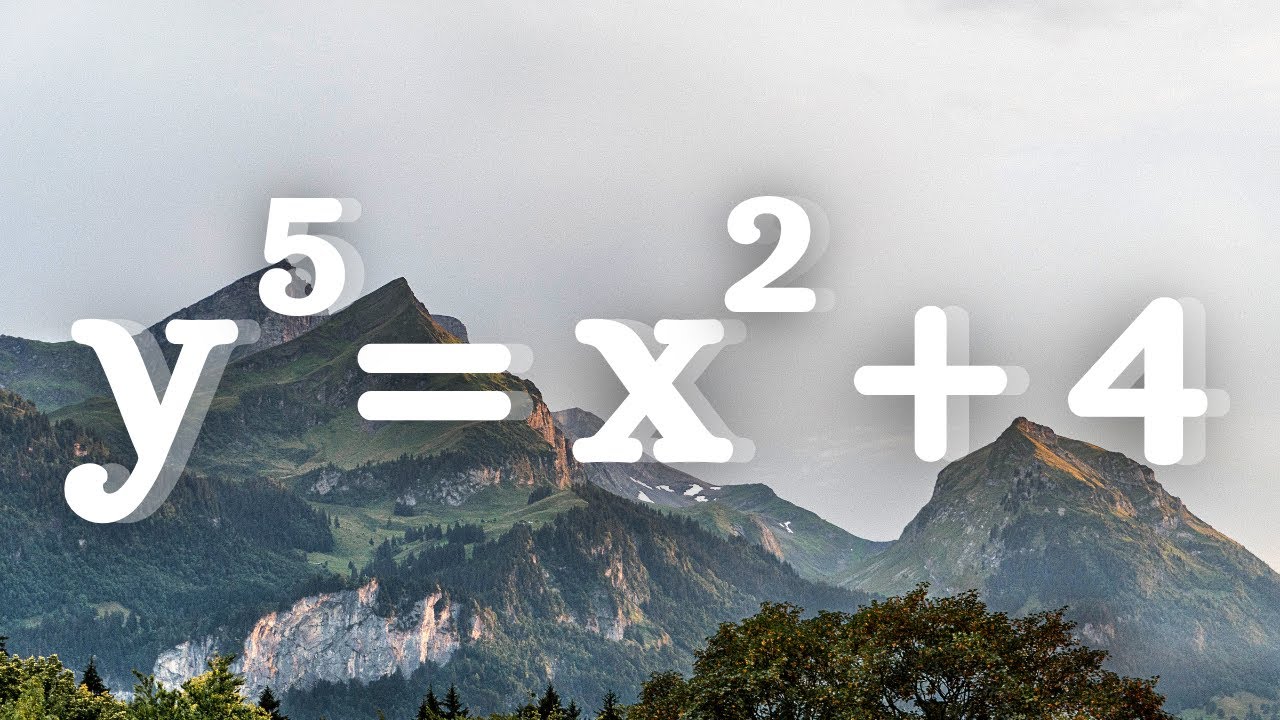
Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
A throwback number theory problem
An awesome number theory contest problem
A cool number theory problem!
A quick number theory problem!
two number theory problems
JBMO 2001 - P1: A good beginner number theory problem
A Number Theory Problem from Canadian Math Olympiads
Another quick number theory problem
The smallest such prime...
The foundation -- Number Theory 1
IMO Shortlist 2005 - N6: A difficult number theory problem?
An awesome Putnam problem with a number theory twist!
Check out this super classic number theory homework problem!
2023 Number Challenge: Solve the Diophantine Equation, leave your answer in the comments
A nice, quick number theory problem
Simple number theory problem
A nice number theory problem from an Argentinian math olympiad
Ducky first meeting with his wife aroob jatoi#makhan
Marie-Sophie Germain: Mathematician - The Brilliance of Marie's Work #shorts #MarieSophieGermai...
Random Math Problem: Number Theory
Complex Numbers Example: Graphing & Arithmetic; FE-Approved Casio Calculator Storage & Manip...
Salsa Night in IIT Bombay #shorts #salsa #dance #iit #iitbombay #motivation #trending #viral #jee
IMO 2023/3: IS IT NUMBER THEORY?
Speed running two number theory problems
Комментарии
 0:11:13
0:11:13
 0:14:16
0:14:16
 0:10:41
0:10:41
 0:07:00
0:07:00
 0:09:44
0:09:44
 0:11:55
0:11:55
 0:08:29
0:08:29
 0:07:50
0:07:50
 0:16:44
0:16:44
 0:19:53
0:19:53
 0:06:47
0:06:47
 0:08:53
0:08:53
 0:09:58
0:09:58
 0:00:56
0:00:56
 0:07:58
0:07:58
 0:02:14
0:02:14
 0:11:04
0:11:04
 0:00:20
0:00:20
 0:00:44
0:00:44
 0:04:10
0:04:10
 0:29:45
0:29:45
 0:00:14
0:00:14
 1:34:36
1:34:36
 0:14:00
0:14:00