filmov
tv
An awesome number theory contest problem

Показать описание
🌟Support the channel🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
🌟my other channels🌟
🌟My Links🌟
🌟How I make Thumbnails🌟
🌟Suggest a problem🌟
An awesome number theory contest problem
basic number theory facts for math competition (Berkeley mini Math Tournament)
How to prepare for Number Theory at Math Competitions and the International Math Olympiad?
An awesome number theory problem
A quick New Zealand number theory problem
An awesome Putnam problem with a number theory twist!
The High Schooler Who Solved a Prime Number Theorem
Number Theory by George Andrews #shorts
A cool number theory problem!
The 7 Levels of Math
When mathematicians get bored (ep1)
The foundation -- Number Theory 1
Greatest Mathematician of All Time #shorts
How Real Math Nerds Do It
How REAL Men Integrate Functions
Proof Based Linear Algebra Book
Bill Gates Vs Human Calculator
Algebraic number theory - an illustrated guide | Is 5 a prime number?
Maths vs Physics
Number Theory Book for Self-Study
A team selection number theory problem.
Luxembourg - Math Olympiad Question | You should know this trick
The Most Efficient Way for Beginners to Start Understanding Number Theory!
FUN Ecuadorian Math Olympiad Number Theory Problem
Комментарии
 0:14:16
0:14:16
 0:16:15
0:16:15
 0:04:59
0:04:59
 0:10:19
0:10:19
 0:00:41
0:00:41
 0:08:53
0:08:53
 0:05:15
0:05:15
 0:00:19
0:00:19
 0:10:41
0:10:41
 0:08:44
0:08:44
 0:00:37
0:00:37
 0:19:53
0:19:53
 0:00:45
0:00:45
 0:00:15
0:00:15
 0:00:35
0:00:35
 0:00:24
0:00:24
 0:00:51
0:00:51
 0:20:31
0:20:31
 0:00:25
0:00:25
 0:00:41
0:00:41
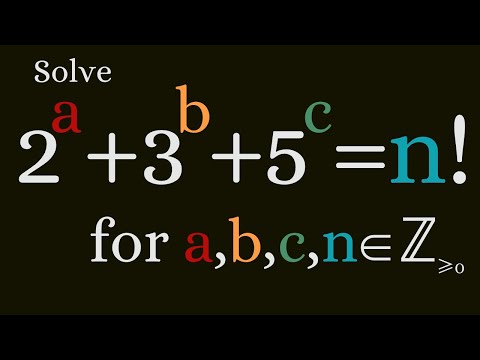 0:13:41
0:13:41
 0:02:51
0:02:51
 0:02:29
0:02:29
 0:19:50
0:19:50