filmov
tv
The hidden link between Prime Numbers and Euler's Number

Показать описание
We will discuss how miraculously Euler's Number appears when asking how many factors a number has on average, which is closely related to the distribution of prime numbers. I still remember how amazed I was, when I first learned about this fact, so I had to share it with the world.
The hidden link between Prime Numbers and Euler's Number
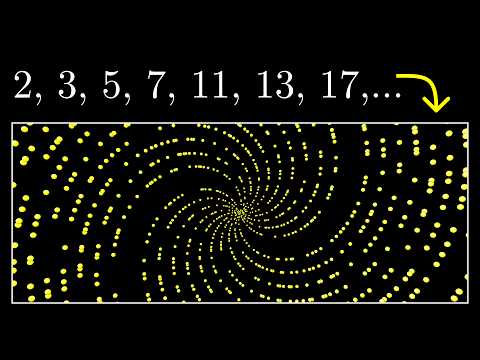
Why do prime numbers make these spirals? | Dirichlet’s theorem and pi approximations
The Riemann Hypothesis, Explained
Major VFX error in Deadpool And Wolverine movie 😱🤯 ! #deadpoolandwolverine #marvel #wolverine #mcu...
They’re both so cute behind the scenes 💗| Hidden Love | YOUKU Shorts
The HIDDEN LINK Between SoFi and Amazon! [AMZN Stock x SOFI Stock SECRETS Revealed]
The HIDDEN LINK between ELON MUSK & SOFI: Anthony Noto is TAKING SOFI STOCK to the MOON! 🚀
Dijkstra's Hidden Prime Finding Algorithm
Spot The Hidden People For $10,000
Apple watch hidden camera
He really think she is cute 💕| Hidden Love | YOUKU Shorts
Roku Hidden Menu
The magic of Fibonacci numbers | Arthur Benjamin | TED
Hidden Speaker Prank On Boyfriend🤣👻… #shorts
The hidden link between mental health and addiction explained
NADIA'S HIDDEN TALENT 😳
UFOs & Religion: Vatican Reveals Hidden Link (ft. Diana Pasulka)
Windows has a hidden malware removal tool | #shorts #trending #mrt #malware
Why the bond markets think inflation is coming back
Secret Items Hidden in Go Goated!
EA fc Mobile Hidden skills 🔥🔥 ft rabona and more #fifamobile #fcmobile #pele #cr7 #messi
Hidden Steam Deck OLED Features
The hidden cost of using a debit card 💳
Covenant's Hidden Power Armor in Fallout 4
Комментарии
 0:12:29
0:12:29
 0:22:21
0:22:21
 0:16:24
0:16:24
 0:00:42
0:00:42
 0:00:27
0:00:27
 0:08:30
0:08:30
 0:06:10
0:06:10
 0:15:48
0:15:48
 0:00:35
0:00:35
 0:00:34
0:00:34
 0:00:17
0:00:17
 0:00:26
0:00:26
 0:06:25
0:06:25
 0:00:39
0:00:39
 0:01:27
0:01:27
 0:00:20
0:00:20
 1:28:50
1:28:50
 0:00:17
0:00:17
 0:08:20
0:08:20
 0:00:32
0:00:32
 0:00:22
0:00:22
 0:00:27
0:00:27
 0:00:44
0:00:44
 0:00:19
0:00:19