filmov
tv
Proving a Nice Inequality in Three Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ProvingInequalities
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
#ChallengingMathProblems #ProvingInequalities
via @YouTube @Apple @Desmos @NotabilityApp
@googledocs @canva
PLAYLISTS 🎵 :
Proving a Nice Inequality in Three Ways
Proving a nice inequality
Introduction to Inequality Proofs
Proving a quick easy inequality #shorts
Inequality Mathematical Induction Proof: 2^n greater than n^2
Mediant Inequality I
Proving a Nice Trigonometric Inequality | #Trigonometry
Visual Cauchy-Schwarz Inequality
Structurally Unsound: Social inequalities in the mid-2020s
Proving a Quick and Easy Inequality
Proving an Inequality Using Inequalities
Induction: Inequality Proofs
Can you prove this Inequality?
Inequality Proofs (5 of 5: Using Calculus to prove an inequality)
Proving the Inequality a(a+b)+b(b+1) ≥ -1/3
A Simple Way to Prove This Inequality | Olympiad Math
S01.10 Bonferroni's Inequality
This Inequality Is Like No Other
Proof: Triangle Inequality Theorem | Real Analysis
AM-GM inequality visually
AM-GM Inequality II
Triangle Inequality for Real Numbers Proof
Bernoulli's Inequality: A Speedy Proof
⚠️TRIANGLE INEQUALITY PROOF in 1 MINUTE, Real numbers, Calculus inequalities, #shorts
Комментарии
 0:08:34
0:08:34
 0:06:20
0:06:20
 0:12:05
0:12:05
 0:00:32
0:00:32
 0:09:20
0:09:20
 0:00:57
0:00:57
 0:04:41
0:04:41
 0:01:01
0:01:01
 1:14:59
1:14:59
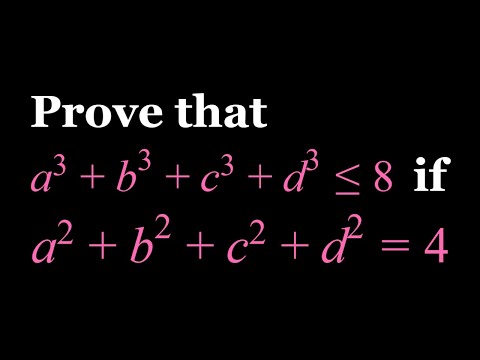 0:05:38
0:05:38
 0:14:50
0:14:50
 0:14:30
0:14:30
 0:08:02
0:08:02
 0:07:41
0:07:41
 0:07:30
0:07:30
 0:06:20
0:06:20
 0:09:28
0:09:28
 0:00:17
0:00:17
 0:05:30
0:05:30
 0:01:00
0:01:00
 0:00:55
0:00:55
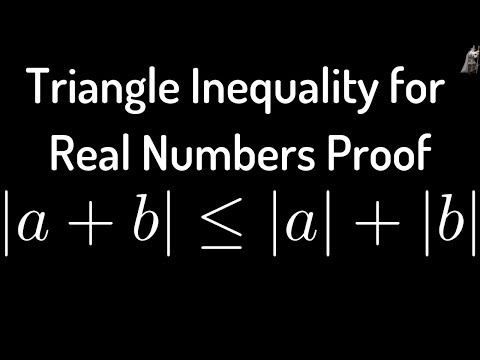 0:03:08
0:03:08
 0:00:57
0:00:57
 0:00:59
0:00:59