filmov
tv
Proof: Triangle Inequality Theorem | Real Analysis

Показать описание
The absolute value of a sum is less than or equal to the sum of the absolute values for any two real numbers. That is: |a+b| is less than or equal to |a|+|b|. This is called the triangle inequality. It's very useful in real analysis and we'll prove it in today's lesson! The name of the theorem is explained a little below.
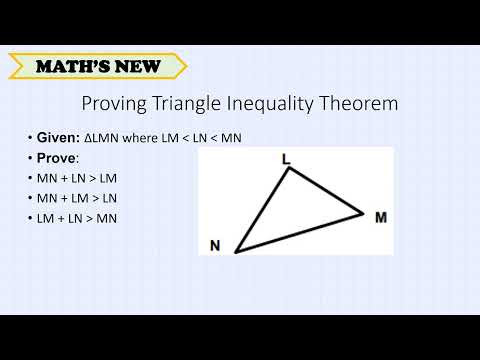
If we considered a triangle made of vectors x, y, and z, with x and z starting at the origin, then the vector z is the vector x+y, and thus the theorem says this third side (z) of the triangle must be no greater than the sum of the other two sides: |z| is less than or equal to |x| + |y| and since the vector z is the vector x+y we have |x+y| is less than or equal to |x| + |y|. Speaking strictly in terms of geometry, we'd often use a strictly less than inequality for this theorem because the equality case describes a "degenerate" triangle, where the "triangle" is just a line. However, the "less than or equal to" inequality is perfectly valid and reasonable for real numbers.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
If we considered a triangle made of vectors x, y, and z, with x and z starting at the origin, then the vector z is the vector x+y, and thus the theorem says this third side (z) of the triangle must be no greater than the sum of the other two sides: |z| is less than or equal to |x| + |y| and since the vector z is the vector x+y we have |x+y| is less than or equal to |x| + |y|. Speaking strictly in terms of geometry, we'd often use a strictly less than inequality for this theorem because the equality case describes a "degenerate" triangle, where the "triangle" is just a line. However, the "less than or equal to" inequality is perfectly valid and reasonable for real numbers.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
********************************************************************
The outro music is by a favorite musician of mine named Vallow, who, upon my request, kindly gave me permission to use his music in my outros. I usually put my own music in the outros, but I love Vallow's music, and wanted to share it with those of you watching. Please check out all of his wonderful work.
********************************************************************
+WRATH OF MATH+
Follow Wrath of Math on...
Комментарии
 0:05:30
0:05:30
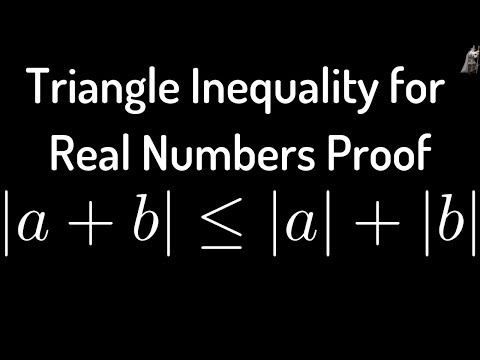 0:03:08
0:03:08
 0:05:52
0:05:52
 0:08:53
0:08:53
 0:03:10
0:03:10
 0:07:27
0:07:27
 0:18:38
0:18:38
 0:07:16
0:07:16
 1:50:00
1:50:00
 0:30:20
0:30:20
 0:08:45
0:08:45
 0:09:24
0:09:24
 0:13:08
0:13:08
 0:04:10
0:04:10
 0:05:10
0:05:10
 0:13:28
0:13:28
 0:04:28
0:04:28
 0:01:38
0:01:38
 0:06:58
0:06:58
 0:01:25
0:01:25
 0:01:55
0:01:55
 0:05:04
0:05:04
 0:03:37
0:03:37
 0:03:11
0:03:11