filmov
tv
Proving an Inequality Using Inequalities
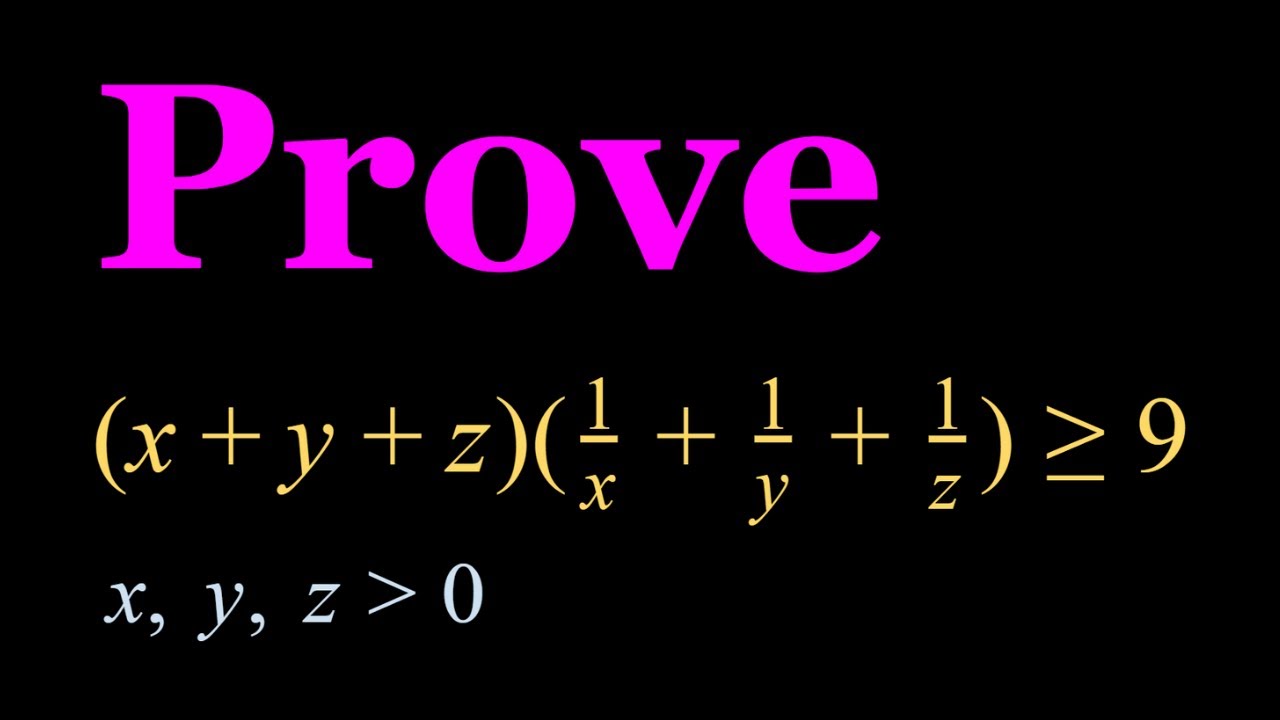
Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #ProvingInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #ProvingInequalities
EXPLORE 😎:
PLAYLISTS 🎵 :
Proving an Inequality Using Inequalities
Induction with inequalities
Induction: Inequality Proofs
Proving Algebraic Inequalities (1 of 3: Introductory principles)
Induction Proofs Involving Inequalities.
Inequality Mathematical Induction Proof: 2^n greater than n^2
Discrete Math - 5.1.2 Proof Using Mathematical Induction - Inequalities
Inequalities for Math Olympiad: Prove an Inequality
How to prove inequalities using a basic one.
Principle of Mathematical Induction Inequality Proof Video
Proofs involving Inequalities
2^n is greater than n^2. Strategy for Proving Inequalities. [Mathematical Induction]
Proof by Induction | Inequalities Proof
Inequality Proofs: Multiplication & Division of Inequalities
Proving Inequalities using Linear Algebra
401R3.1 Solving vs Proving Inequalities
Proof of Bernoulli's Inequality using Mathematical Induction
Proof by Induction - Inequalities
Inequalities for Math Olympiad: Prove an inequality ln 2 \lt 1/(n+1) + ... + 1/(3n) \lt ln 3
Induction Inequality Proof Example 3: 5^n + 9 less than 6^n
Induction Inequality Proof: 3^n is greater than or equal to 2n + 1
Algebra 3 - Proving Abstract Inequalities
L18.3 The Chebyshev Inequality
5 simple unsolvable equations
Комментарии
 0:14:50
0:14:50
 0:04:07
0:04:07
 0:14:30
0:14:30
 0:09:37
0:09:37
 0:06:34
0:06:34
 0:09:20
0:09:20
 0:09:53
0:09:53
 0:04:16
0:04:16
 0:00:30
0:00:30
 0:05:54
0:05:54
 0:04:44
0:04:44
 0:09:22
0:09:22
 0:04:17
0:04:17
 0:12:31
0:12:31
 0:12:32
0:12:32
 0:23:31
0:23:31
 0:05:42
0:05:42
 0:05:32
0:05:32
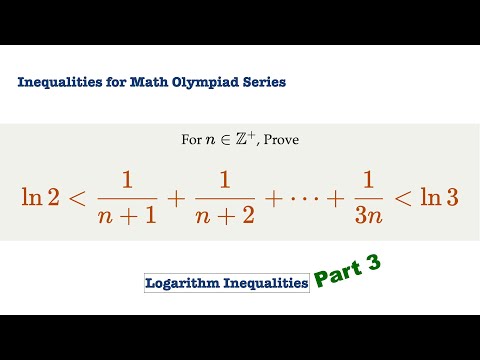 0:09:10
0:09:10
 0:10:42
0:10:42
 0:08:49
0:08:49
 0:10:06
0:10:06
 0:05:57
0:05:57
 0:00:50
0:00:50