filmov
tv
Visual Cauchy-Schwarz Inequality
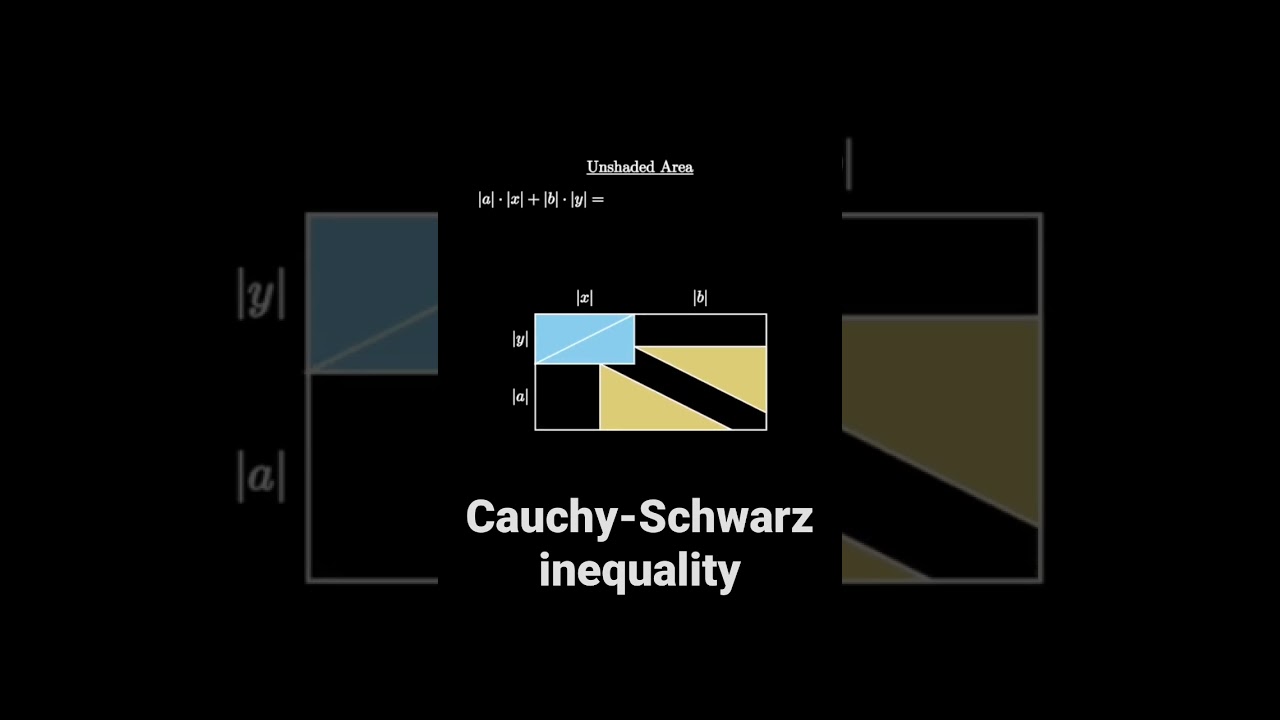
Показать описание
This is a short, animated visual proof of the two-dimensional Cauchy-Schwarz inequality (sometimes called Cauchy–Bunyakovsky–Schwarz inequality) using the Side-angle-side formula for the area of a parallelogram.
To learn more about animating with manim, check out:
#math #inequality #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #algebra #areas #mathematics #cauchyschwarz #algebraicidentity #mathshorts #mathvideo #mtbos
To learn more about animating with manim, check out:
#math #inequality #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #algebra #areas #mathematics #cauchyschwarz #algebraicidentity #mathshorts #mathvideo #mtbos
Visual Cauchy-Schwarz Inequality
Cauchy Bunyakovsky Schwarz Inequality I (visual proof)
Cauchy-Bunyakovsky-Schwarz Inequality II (visual proof)
A Visual Proof of the Cauchy Schwarz Inequality
Basic Cauchy-Schwarz Inequality - Linear Algebra Made Easy (2016)
Cauchy-Schwarz is the way!
The Cauchy Schwartz Inequality
Functional Analysis 10 | Cauchy-Schwarz Inequality
The Cauchy-Schwarz Inequality
Cauchy-Schwarz Inequality Proof
Cauchy Schwarz Inequality Through Projection
Cauchy-Schwartz Inequality Proof Using Inner Product and Complex Analysis
Cauchy Schwarz Inequality | Applications to Problems, and When Equality Occurs
Cauchy Schwarz Application
Proving Cauchy-Schwartz Inequality
Cauchy Schwarz and Triangle Inequalities proof
The cauchy Bunyakowsky Schwarz Inequality
Proving the Cauchy–Schwarz Inequality for Vectors in R^n
The Cauchy-Schwarz Inequality Part 1
05 - Cauchy Schwartz inequality and proof
New Geometrical Proof of Cauchy Schwarz Inequality with Carmen
Cauchy Shwartz Inequality Problem 1 - Vector Spaces - Engineering Mathematics - 4
Cauchy Schwarz and what to DO with it (corrected) // An Introduction to Real Analysis
Theorem 3.2.4 (Cauchy-Schwarz Inequality)
Комментарии
 0:01:01
0:01:01
 0:01:47
0:01:47
 0:02:05
0:02:05
 0:05:35
0:05:35
 0:02:19
0:02:19
 0:00:28
0:00:28
 0:14:37
0:14:37
 0:10:06
0:10:06
 0:09:17
0:09:17
 0:10:47
0:10:47
 0:07:10
0:07:10
 0:13:08
0:13:08
 0:10:16
0:10:16
 0:05:21
0:05:21
 0:00:54
0:00:54
 0:02:37
0:02:37
 0:10:26
0:10:26
 0:07:00
0:07:00
 0:15:07
0:15:07
 0:10:41
0:10:41
 0:02:18
0:02:18
 0:03:19
0:03:19
 0:12:47
0:12:47
 0:11:45
0:11:45