filmov
tv
Triangle Inequality for Real Numbers Proof

Показать описание
Triangle Inequality for Real Numbers Proof
Triangle Inequality for Real Numbers Proof
Proof: Triangle Inequality Theorem | Real Analysis
General Triangle Inequality for Real Numbers
Triangle inequality for real numbers proof
Fast proof of triangle inequalities for real numbers
Real Analysis Course #10 - The Triangle Inequality
Triangular inequality Proof (easy method)
Prove the Triangle Inequality (Real Number Case)
The limit of sin(1/x) as x approaches 0 does not exist (Proof) [ILIEKMATHPHYSICS]
The Triangle inequality on The Real Numbers
The Triangle Inequality for Real Numbers (Proof) | Real Analysis
Triangle Inequality
Real analysis | Triangle inquality
Triangle Inequality Proof: |x+y| less than or equal to |x|+|y|
How to Prove the Triangle Inequality for Complex Numbers
⚠️TRIANGLE INEQUALITY PROOF in 1 MINUTE, Real numbers, Calculus inequalities, #shorts
Reverse Triangle Inequality for Real Numbers
Triangle Inequality Proof
Reverse Triangle Inequality for Real Numbers (Proof) | Real Analysis
Triangle Inequality for Complex Numbers
Prove the Triangle Inequality for Complex Numbers
Ext2 Inequalities: The (ℝeal) Triangle Inequalities
Proof of the Triangle Inequality for real numbers (|a + b| ≤ |a| + |b|) [ILIEKMATHPHYSICS]
Triangle Inequality of Complex Number
Комментарии
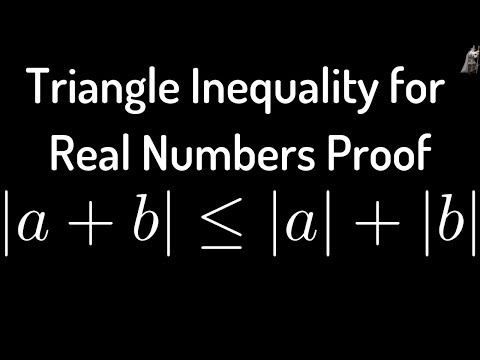 0:03:08
0:03:08
 0:05:30
0:05:30
 0:12:13
0:12:13
 0:03:08
0:03:08
 0:05:23
0:05:23
 0:04:22
0:04:22
 0:05:10
0:05:10
 0:14:19
0:14:19
 0:08:46
0:08:46
 0:06:05
0:06:05
 0:04:07
0:04:07
 0:13:08
0:13:08
 0:07:07
0:07:07
 0:03:11
0:03:11
 0:09:24
0:09:24
 0:00:59
0:00:59
 0:08:12
0:08:12
 0:02:38
0:02:38
 0:03:06
0:03:06
 0:06:55
0:06:55
 0:08:45
0:08:45
 0:14:01
0:14:01
 0:03:20
0:03:20
 0:05:47
0:05:47