filmov
tv
S01.10 Bonferroni's Inequality

Показать описание
MIT RES.6-012 Introduction to Probability, Spring 2018
Instructor: John Tsitsiklis
License: Creative Commons BY-NC-SA
Instructor: John Tsitsiklis
License: Creative Commons BY-NC-SA
S01.10 Bonferroni's Inequality
Bonferroni's inequality proof
Boole's and Bonferroni's Inequality
Bonferroni Inequality | Question 2 | Chapter 1 | Bayesian Reasoning & Machine Learning
Boole's Inequality: Statement and Proof
Bonferroni's Inequality Proof | 9th Video
Theorem: Boole's Inequality || Ch: Elements Of Probability Theory || Class: B.sc/ B.A. 5th Seme...
Boole's inequality
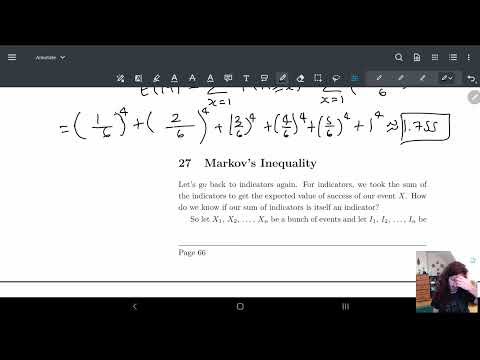
27 Markov's Inequality | Boole's inequality, Markov's inequality, Example
Ch4_3: Diagnostic Checking F Test Bonferroni t-Test of Single Factor Experiments PP 19to25
Boole’s inequality proof
Boole's Inequality with Complete Proof | BSc. Statistics #statistics #probability #mathematics ...
Lecture 5: g. Monotonicity, boundedness, Boole's inequality — [Probability | Santosh S. Venkat...
ANOVA Part IV: Bonferroni Correction | Statistics Tutorial #28 | MarinStatsLectures
Day 29: Why Bonferroni doesn't work well in imaging
Probability theory L-8 , Boole's inequality for n events complete proof
Boole's Inequality with Proof || IN HINDI || EASY EXPLAIN
The Bonferroni Correction
Boole's inequality
Proof of Bernoulli's Inequality using Mathematical Induction
Bonferroni Multiple Comparisons
Lecture 2: Hoeffding's Inequality
bernoulli inequality proof by induction
Holders inequality usage
Комментарии
 0:09:28
0:09:28
 0:09:28
0:09:28
 0:10:28
0:10:28
 0:02:32
0:02:32
 0:07:26
0:07:26
 0:04:24
0:04:24
 0:00:05
0:00:05
 0:01:33
0:01:33
 0:10:25
0:10:25
 0:13:38
0:13:38
 0:11:16
0:11:16
 0:17:35
0:17:35
 0:09:47
0:09:47
 0:16:55
0:16:55
 0:14:07
0:14:07
 0:05:55
0:05:55
 0:07:30
0:07:30
 0:03:20
0:03:20
 0:07:10
0:07:10
 0:05:42
0:05:42
 0:18:33
0:18:33
 0:28:07
0:28:07
 0:06:35
0:06:35
 0:12:10
0:12:10