filmov
tv
Solving A Functional System of Equations in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Solving A Functional System of Equations in Two Ways
Solving A Functional System of Equations in Two Ways
Solving a Functional System of Equations
A Quick and Easy Functional Equation
Solving a Functional Equation
Solving Another Functional System of Equations in Two Ways
Solving a Quick and Easy Functional Equation
A Polynomial Functional System of Equations
Quadratic Equations Amazing Strategy with Perfect Squares on Each Side
A Nice and Easy Functional Equation
How do we solve a system of linear equations using any method
A Functional Equation from Putnam and Beyond
Solving A Functional System #algebraequations #maths #functions
Solving A Nice Functional Equation
a functional equation /functional equation
A Functional Equation from Samara Math Olympiads
Algebra Solving a Functional Equation Example
Solving an Interesting Functional Equation
Solving A Functional Equation
functional equations/solving a functional equation
Solving Systems of Equations By Graphing
How To Solve A Functional Equation | The Easy Way
Have You Solved a Functional Equation Before?
Solving a Functional Equation by Elimination
Комментарии
 0:09:27
0:09:27
 0:09:27
0:09:27
 0:02:39
0:02:39
 0:06:49
0:06:49
 0:10:36
0:10:36
 0:05:40
0:05:40
 0:05:47
0:05:47
 0:08:49
0:08:49
 0:04:38
0:04:38
 0:05:07
0:05:07
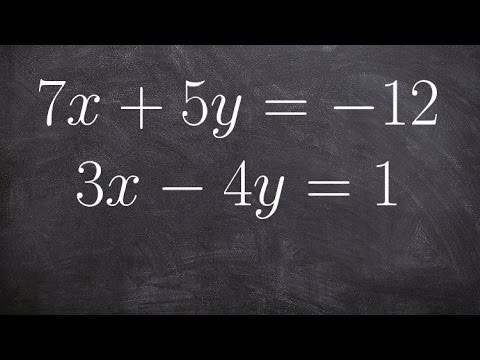 0:04:34
0:04:34
 0:12:07
0:12:07
 0:00:40
0:00:40
 0:09:50
0:09:50
 0:04:42
0:04:42
 0:08:47
0:08:47
 0:01:37
0:01:37
 0:09:49
0:09:49
 0:11:58
0:11:58
 0:05:06
0:05:06
 0:05:15
0:05:15
 0:07:19
0:07:19
 0:00:40
0:00:40
 0:09:08
0:09:08