filmov
tv
A Polynomial Functional System of Equations

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Polynomial Functional System of Equations
What is a polynomial function
Polynomial Functions and Power Functions
Polynomial Hack: Identify a Polynomial from Just Two Inputs // #SoME2
Finding All Zeros of a Polynomial Function Using The Rational Zero Theorem
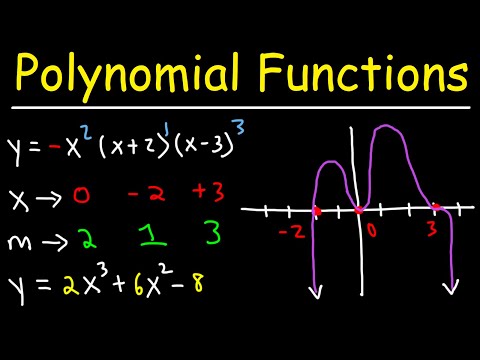
How To Graph Polynomial Functions Using End Behavior, Multiplicity & Zeros
A Polynomial System in Three Variables
Finding All of the Zeros of a Polynomial Including Complex
Exponential equation. #maths #Mathematics #mathstutor #mathsisfun #exponential
How To Find The Polynomial Function From a Graph
Writing Polynomial Functions With Given Zeros | Precalculus
Determining if a function is a polynomial or not then determine degree and LC
Polynomial Function - Complex Factorization Theorem
Definition of a Polynomial Function Equation : Math Definitions & More
Domain of a Polynomial Function
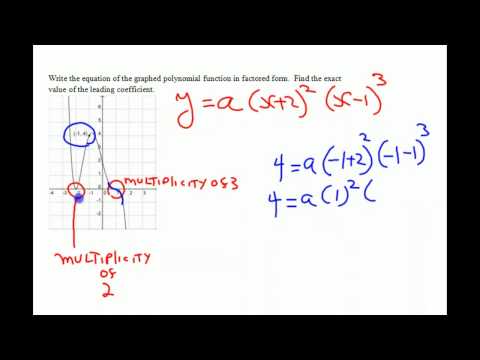
Finding the equation of the graph of a polynomial function
Class 12th – Polynomial Function | Continuity and Differentiability | Tutorials Point
Turning Points and X Intercepts of a Polynomial Function
Write a polynomial function f of least degree that has rational coefficients, a leading. | Plainmath
AP Precalculus – 1.5A Polynomial Functions and Complex Zeros
SAT Math Polynomial Functions
Ex1: Find an Equation of a Degree 4 Polynomial Function From the Graph of the Function
Polynomial Approximations
Given a Polynomial Function Find All of the Zeros
Комментарии
 0:08:49
0:08:49
 0:04:31
0:04:31
 0:05:55
0:05:55
 0:13:49
0:13:49
 0:12:18
0:12:18
 0:20:28
0:20:28
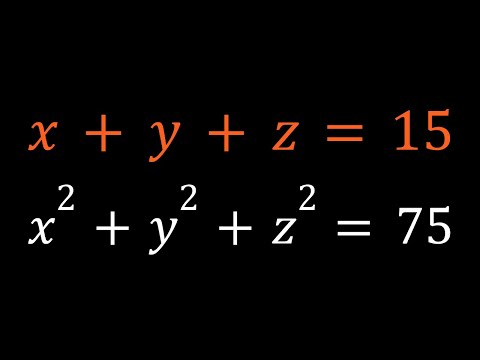 0:11:20
0:11:20
 0:05:35
0:05:35
 0:01:01
0:01:01
 0:10:04
0:10:04
 0:17:00
0:17:00
 0:09:53
0:09:53
 0:11:26
0:11:26
 0:01:28
0:01:28
 0:00:55
0:00:55
 0:03:32
0:03:32
 0:07:43
0:07:43
 0:05:32
0:05:32
 0:02:00
0:02:00
 0:27:48
0:27:48
 0:01:00
0:01:00
 0:04:05
0:04:05
 0:09:17
0:09:17
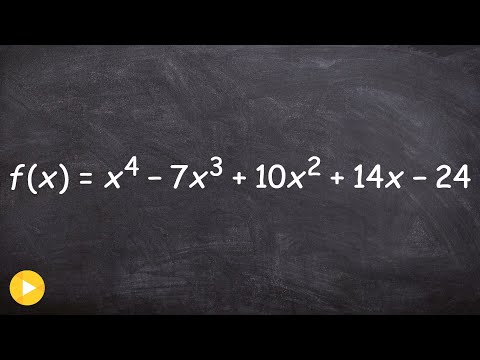 0:11:31
0:11:31