filmov
tv
Solving Another Functional System of Equations in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
#ChallengingMathProblems #FunctionalEquations
PLAYLISTS 🎵 :
Solving Another Functional System of Equations in Two Ways
Solving A Functional System of Equations in Two Ways
Solving A Functional System of Equations in Two Ways
Solving A Functional System of Equations
Solving a Functional System of Equations
Solving a Quick and Easy Functional Equation
Solving an Interesting Functional Equation with 2 Variables | Math Olympiad Problem | Solve For f(x)
Solving A Functional System #algebraequations #maths #functions
Solving Systems of Equations by Substitution | Math Tutorial | Prime path #facts #algebra #maths
Solving equation involving function and inverse
Solving a Radical Functional Equation in Two Ways
Unit 4 4 13 Solving Another Reciprocal Function Using your Calculator
A Problem of Function | 3 Different Methods to Solve
how to solve function systems
Solving Two Functional Equations
Olympiad Challenge! Solve this function Equation | Easy & In-Depth Explanation
Solving a Functional Equation
in to function Type of function Math Solved
Solving A Quick and Fun Functional Equation
Solving a Nice Functional Problem from Russia | Math Olympiad Problem | Simple Functional Question
Solving an Interesting Functional Equation
Solution to functional equation f((x-1)/x) + f(x) = 2x + 4
Solving a Quick and Easy Functional Equation
Math 10 3.1 Example 11 Evaluating and Solving a Tabular Function
Комментарии
 0:05:40
0:05:40
 0:09:27
0:09:27
 0:09:27
0:09:27
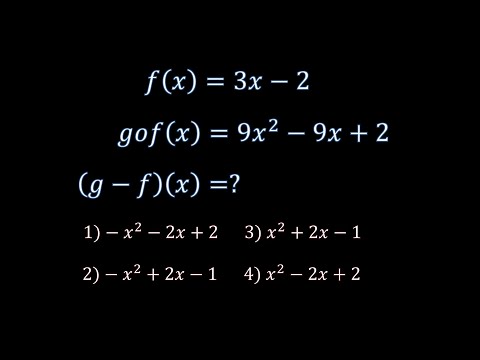 0:02:41
0:02:41
 0:02:39
0:02:39
 0:05:47
0:05:47
 0:03:13
0:03:13
 0:00:40
0:00:40
 0:00:48
0:00:48
 0:02:24
0:02:24
 0:09:16
0:09:16
 0:03:00
0:03:00
 0:10:29
0:10:29
 0:00:36
0:00:36
 0:08:50
0:08:50
 0:12:52
0:12:52
 0:10:36
0:10:36
 0:00:28
0:00:28
 0:03:56
0:03:56
 0:02:46
0:02:46
 0:09:49
0:09:49
 0:07:43
0:07:43
 0:06:19
0:06:19
 0:02:34
0:02:34