Relative Extrema Optimization

In theory and applications, we often want to maximize or minimize some quantity. For example, an engineer may want to maximize the speed of a new computer. A manufacturer may want to maximize profits and market share or minimize cost. A student may want to maximize a grade in calculus or minimize the hours of study needed to earn a particular grade. Without calculus, we only know how to find the optimum points in a few specifics situations (for example, we know how to find the vertex of a parabola). But what if we need to optimize an unfamiliar function?

Calculus provides ways of narrowing the number of points we need to examine to find the exact locations of maximums and minimums and this is what we will be discussing in this lesson.

Learning Objectives:
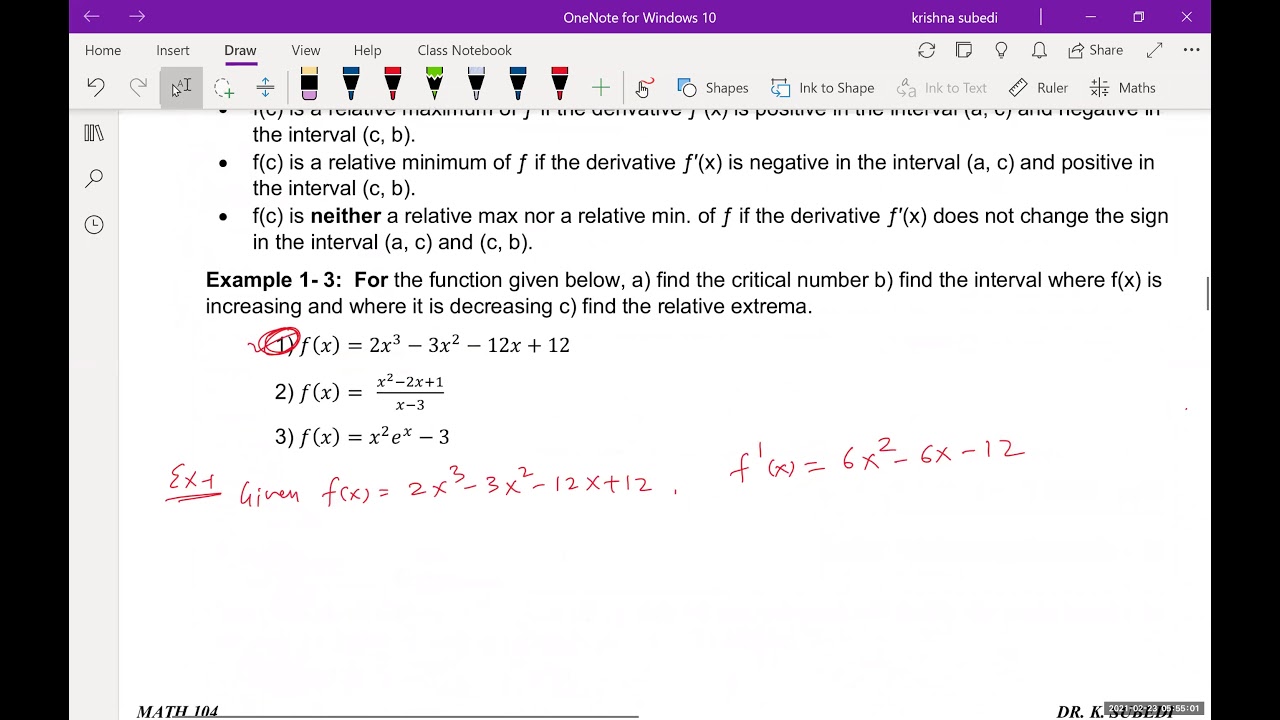
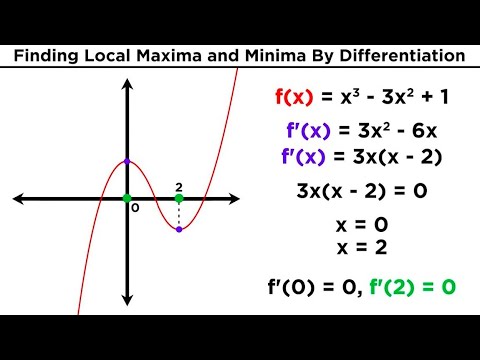
(a) Find critical numbers for a function and the interval where the function is increasing and decreasing
(b) Find relative extrema of a function using the first and second derivative test.