filmov
tv
Multi-variable Optimization & the Second Derivative Test

Показать описание
Finding Maximums and Minimums of multi-variable functions works pretty similar to single variable functions. First,find candidates for maximums/minimums by finding critical points. Critical Points are where the partial derivatives with respect to x and y are both zero. Then we classify each critical point using the second derivative test. In the multivariable case, there is a new option beyond max/min/neither, there is also the case of the saddle point. The second derivative test involves computing the Hessian, the determinant of a matrix that helps decide whether points are maximums/minimums/saddle or inconclusive. We sketch the geometric intuition behind the Hessian.
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
****************************************************
YOUR TURN! Learning math requires more than just watching videos, so make sure you reflect, ask questions, and do lots of practice problems!
****************************************************
****************************************************
Other Course Playlists:
***************************************************
► Want to learn math effectively? Check out my "Learning Math" Series:
►Want some cool math? Check out my "Cool Math" Series:
****************************************************
*****************************************************
This video was created by Dr. Trefor Bazett. I'm an Assistant Teaching Professor at the University of Victoria.
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
Комментарии
 0:13:36
0:13:36
 0:14:35
0:14:35
 0:14:53
0:14:53
 0:08:04
0:08:04
 0:15:08
0:15:08
 0:11:00
0:11:00
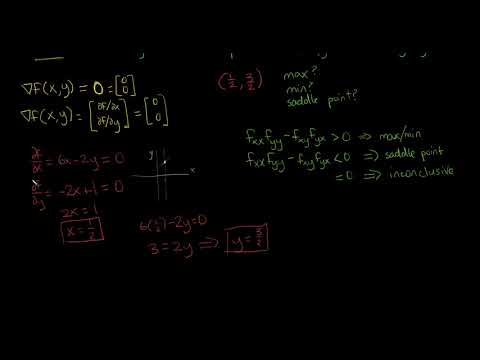 0:10:57
0:10:57
 0:07:20
0:07:20
 1:57:22
1:57:22
 0:11:24
0:11:24
 0:06:10
0:06:10
 0:07:11
0:07:11
 0:08:43
0:08:43
 0:06:29
0:06:29
 0:05:05
0:05:05
 1:00:33
1:00:33
 0:22:38
0:22:38
 0:21:07
0:21:07
 0:08:51
0:08:51
 0:38:15
0:38:15
 0:12:24
0:12:24
 0:11:26
0:11:26
 0:25:31
0:25:31
 0:05:17
0:05:17