Extreme Value Theorem

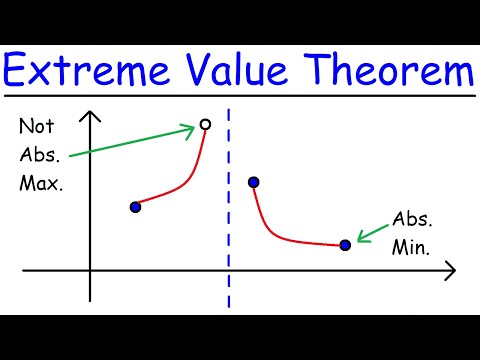
This calculus video tutorial provides a basic introduction into the extreme value theorem which states a function will have a minimum and a maximum value on a closed interval. This video provides graphical examples of absolute extrema and relative extrema. It shows you how to identify the absolute maximum and minimum values of a function on a graph. It also explains how to identify the relative maximum and minimum values as well.

____________________________
Introduction to Limits:

Derivatives - Fast Review:

Introduction to Related Rates:

_____________________________
Extreme Value Theorem:

Finding Critical Numbers:

Local Maximum & Minimum:

Absolute Extrema:

Rolle's Theorem:

________________________________
Mean Value Theorem:

Increasing and Decreasing Functions:

First Derivative Test:

Concavity & Inflection Points:

Second Derivative Test:

_________________________________
L'Hopital's Rule:

Curve Sketching With Derivatives:

Newton's Method:

Optimization Problems:

_______________________________________
Final Exams and Video Playlists:

Full-Length Videos and Worksheets:

[SNIPE]

Just wanted to say thanks for your videos man! They're super helpful and the way you explain is easy to follow. I can literally type in any concept and you've made a video for it. amazing!

[Zenbeau]

you are DOING GOD's WORK. You have a video on everything that's in my first year uni calculus course

[Dmangames-ggcl]

Love these videos. very helpful for night before cramming for calculus mid term

[georgesadler]

MR. Organic Chemistry Tutor, thank you for a solid explanation of the Extreme Value Theorem. This is another important theorem in Calculus/Advanced Calculus. This is an error free video/lecture on YouTube TV with the Organic Chemistry Tutor.

[Sabineee]

A question in my maths textbook told me to comment on "extreme values". So here I am!

[azaa]

4:38 Reasoning for no absolute minimum on left graph: the interval isn't closed at points a and b. // a and b are at open intervals and therefore can't have absolute maximums or minimums. if a was a closed point, then it would be abs. minimum

On right graph, b represents an abs minimum because it's lowest point AND has closed interval. C is not abs max, because its an open circle.

5:13 right graph, the EVT doesnt apply here because there is a break in the graph, therefore no closed interval

[krovely]

you are the best, you always have a video on literally anything I search

[aguilarexequielandrew]

keep doing what youre doing! helps alot <3

[zeroblade]

question if u had a horizontal line at a closed interval[a, b] EVT says there should be a max and a min right, but there isn't one, in that case right?

[HDitzzDH]

5:30 Wouldn't f(d) be considered a local maximum since that is an endpoint?

[felipenetto]

What if the function is for example y=1? it is continuous for every xER and it has neither max and mins

[emmanuelssali]

Thanks a lot. But how would I tell if a graph contains open circles or closed circles?

[explorerofworlds]

Shouldn't this be called the definition of extreme values & not the extreme values? There's no proof you can make for this. It seems like we literally define relative mins & maxs values as points at which x equals 0 between an decreasing & increasing slope. We do the same for absolute max & min as the largest possible value of our function i.e if there is a maximum or minimum value to the function.

[daizybaby]

really bad never understood anything from the video!!!! and never did