filmov
tv
Proof that the Sequence (-1)^n Diverges using the Definition

Показать описание
Proof that the Sequence (-1)^n Diverges using the Definition
Proof: Sequence 1/n Converges to 0 | Real Analysis Exercises
Proof: Sequence (-1)^n Diverges | Real Analysis
Proof that the Sequence (-1)^n Diverges using the Definition
Proof: Sequence (1/n) is a Cauchy Sequence | Real Analysis Exercises
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis
Sequence (1^n) Diverges using Subsequences | Real Analysis
Proof: Sequence 1/sqrt(n) Converges to 0 | Real Analysis
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
Limit of a Sequence Problems | Calculus 2 Exercises
Definition of the Limit of a Sequence | Real Analysis
Determining whether a sequence converges or diverges
Real Analysis Course #15 - Limit of 1/n Converges to 0
Sequence Converges iff Every Subsequences Converge to the Same Limit | Real Analysis
Proof: Sequence {sqrt(n+1)-sqrt(n)} Converges to 0 | Real Analysis Exercises
Sequences (Real Analysis) | SE#7 | Monotone convergence theorem | prove (1+1/n)^n is convergent
Converging and Diverging Sequences Using Limits - Practice Problems
Proof: lim (-1)^n doesn't converge
Proving a Sequence Converges with the Formal Definition Advanced Calculus
Series convergence of 1/n! direct comparison -- difficult proof! Direct comparison sum(1/n!) proof.
Intro to Cauchy Sequences and Cauchy Criterion | Real Analysis
VIDEO - 54 SEQUENCE 1/n IS CAUCHY SEQUENCE #REALANALYSIS #sequence #highermathematics
How to Determine if a Sequence is Bounded using the Definition: Example with a_n = 1/(2n + 3)
Sequences (Real Analysis) | SE#12-13 | Monotone convergence theorem | 1/n+1...+1/n+n & 1/1!+...+...
The Sequence a_n = sin(n)/n Converges or Diverges Two Solutions with Proof
Комментарии
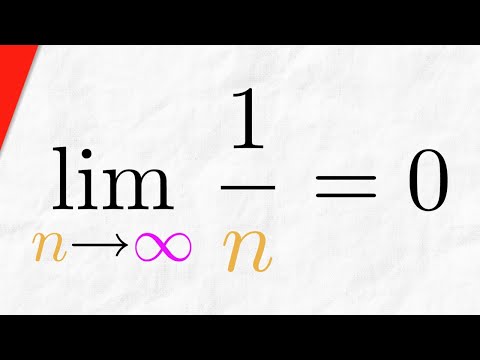 0:06:48
0:06:48
 0:13:07
0:13:07
 0:04:27
0:04:27
 0:08:16
0:08:16
 0:06:43
0:06:43
 0:07:10
0:07:10
 0:07:13
0:07:13
 0:06:53
0:06:53
 0:08:25
0:08:25
 0:13:59
0:13:59
 0:05:39
0:05:39
 0:04:22
0:04:22
 0:08:54
0:08:54
 0:11:06
0:11:06
 0:03:38
0:03:38
 0:30:13
0:30:13
 0:05:37
0:05:37
 0:07:57
0:07:57
 0:04:25
0:04:25
 0:15:53
0:15:53
 0:05:39
0:05:39
 0:02:13
0:02:13
 0:05:34
0:05:34
 0:02:47
0:02:47