filmov
tv
Proof: Sequence (-1)^n Diverges | Real Analysis

Показать описание
We prove the sequence (-1)^n diverges. This is an example of a sequence that diverges, but not to positive or negative infinity. Thus, we will prove it diverges using the plain old definition of divergence - that is, that it does not converge to any real number. To prove (-1)^n doesn't converge to any real number, we will assume for contradiction that it does converge to a real number, and show this forces a contradiction.
In a nutshell, by assuming (-1)^n converges to a limit L, this forces the terms of the sequence to get arbitrarily close to L. Since the sequence alternates between -1 and 1, this means -1 should be arbitrarily close to L and so should 1. This is obviously not possible. For example, 1 and -1 should both be within 1/2 of L, but this means L is both positive and negative. We'll see the details of this contradiction in the full lesson.
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Lyndon for their generous support on Patreon!
Follow Wrath of Math on...
In a nutshell, by assuming (-1)^n converges to a limit L, this forces the terms of the sequence to get arbitrarily close to L. Since the sequence alternates between -1 and 1, this means -1 should be arbitrarily close to L and so should 1. This is obviously not possible. For example, 1 and -1 should both be within 1/2 of L, but this means L is both positive and negative. We'll see the details of this contradiction in the full lesson.
★DONATE★
Thanks to Robert Rennie, Barbara Sharrock, and Lyndon for their generous support on Patreon!
Follow Wrath of Math on...
Proof: Sequence (-1)^n Diverges | Real Analysis
Proof that the Sequence (-1)^n Diverges using the Definition
Sequence (1^n) Diverges using Subsequences | Real Analysis
Harmonic Series | It diverges, but insanely slowly!
Proof: Sequence 1/n Converges to 0 | Real Analysis Exercises
Proof: harmonic series diverges | Series | AP Calculus BC | Khan Academy
Sequences that Diverge to Infinity (Definition) | Calculus, Real Analysis
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis
Limit of a Sequence Problems | Calculus 2 Exercises
Series 1/n (Harmonic Series) diverges Proof |Mad Teacher
Determining whether a sequence converges or diverges
Proof: Sequence n^2 Diverges to Infinity | Real Analysis
151.wk9. using cauchy's condensation test to prove sum 1/n diverges
Sequence (-1)^n Converges or Diverges? Proof |Mad Teacher
Proof: Sequence 1/sqrt(n) Converges to 0 | Real Analysis
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
How to Prove a Sequence Diverges Example with n squared
Converging and Diverging Sequences Using Limits - Practice Problems
If Sequence Diverges to Infinity then so do Subsequences | Real Analysis
Convergence and Divergence - Introduction to Series
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Prove Sequence Diverges with Subsequences | Real Analysis
Series sin(1/n) diverges Proof |Maths |Mad Teacher
Proof: lim (-1)^n doesn't converge
Комментарии
 0:13:07
0:13:07
 0:04:27
0:04:27
 0:07:10
0:07:10
 0:04:39
0:04:39
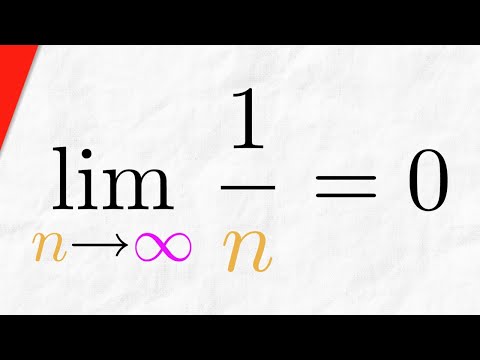 0:06:48
0:06:48
 0:06:33
0:06:33
 0:09:59
0:09:59
 0:06:43
0:06:43
 0:08:25
0:08:25
 0:01:44
0:01:44
 0:05:39
0:05:39
 0:06:02
0:06:02
 0:01:56
0:01:56
 0:04:20
0:04:20
 0:07:13
0:07:13
 0:06:53
0:06:53
 0:03:54
0:03:54
 0:30:13
0:30:13
 0:06:56
0:06:56
 0:16:18
0:16:18
 0:05:36
0:05:36
 0:07:41
0:07:41
 0:04:06
0:04:06
 0:05:37
0:05:37