filmov
tv
Series convergence of 1/n! direct comparison -- difficult proof! Direct comparison sum(1/n!) proof.

Показать описание
Series convergence of 1/n! direct comparison sum(1/n!) approach: we compare to the convergent p-series 1/n^2. This requires showing that n! greater than n^2 when n is sufficiently large, which is a tricky proof because direct comparison with factorials is not simple. In the long run, you're better off using the ratio test in a convergence proof with factorials, but using direct comparison in the convergence with factorials proof here is instructive.
Series convergence of 1/n! direct comparison -- difficult proof! Direct comparison sum(1/n!) proof.
Choosing Which Convergence Test to Apply to 8 Series
Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
Series Comparison Test 1/n! factorial
100 series convergence tests (no food, no water, no stop)
Convergence and Divergence - Introduction to Series
Series of sin(1/n) diverges, Limit comparison test, calculus 2 tutorial
Simple Guide to Series Convergence Tests
KEY 04 – Global Health 2050: The Lancet Commission on Investing in Health 3.0
Direct comparison test with sin(1/n)/n, with geometric construction to show sin(1/n) less than 1/n.
Sum n!/n^n (Series Direct Comparison Test)
Direct Comparison Test - Calculus 2
Series 1/(n+3^n), Direct Comparison Test, calculus 2 tutorial
Determine whether series converges or diverges (-1)^(n+1) 1/(ln n)
series of cos(1/n), test for divergence
Determine if series converges or diverges. {sin(1/n)}. Limit Comparison Test with harmonic series
Series of (1+1/n)^(n^2), root test
Direct comparison test 1/(ln(n)), including derivative proof that ln(n) is less than n. Sum 1/ln(n).
What series convergence test do I use?
Alternating Series Test
Limit Comparison Test
checking for absolute convergence, series of sin(2n)/(1+2^n), calculus 2 tutorial
Determine if series converges. Use test for divergence. cos (1/n)
Limit Comparison Test, Series of 1/(2n+1), calculus 2 tutorial
Комментарии
 0:12:13
0:12:13
 0:43:52
0:43:52
 0:02:26
0:02:26
 6:06:54
6:06:54
 0:16:18
0:16:18
 0:05:36
0:05:36
 0:15:36
0:15:36
 1:37:26
1:37:26
 0:03:08
0:03:08
 0:04:44
0:04:44
 0:15:24
0:15:24
 0:04:32
0:04:32
 0:03:40
0:03:40
 0:02:39
0:02:39
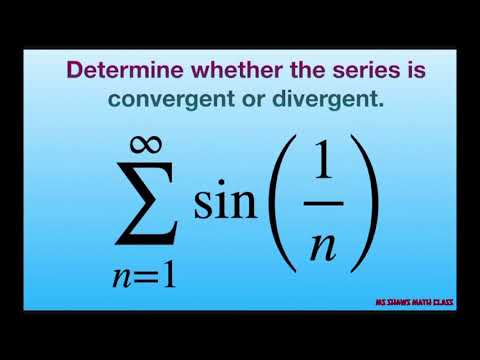 0:04:07
0:04:07
 0:03:23
0:03:23
 0:03:12
0:03:12
 1:36:56
1:36:56
 0:19:41
0:19:41
 0:11:12
0:11:12
 0:05:36
0:05:36
 0:01:42
0:01:42
 0:03:00
0:03:00