Sequence Converges iff Every Subsequences Converge to the Same Limit | Real Analysis

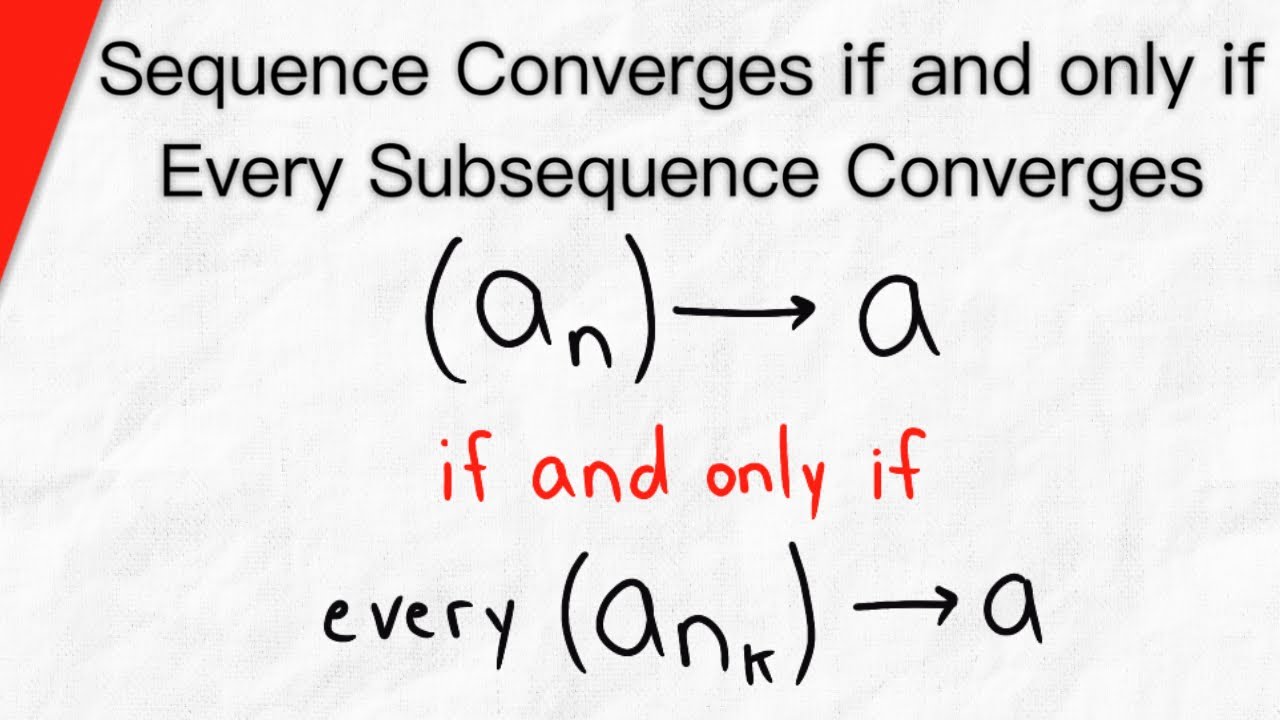
Показать описание

A sequence converges to a limit L if and only if every subsequence converges to L. We prove this wonderful result about subsequences in real analysis in today's video lesson! First we prove that if a sequence converges to a limit, then all of its subsequences converge to that same limit. To do this, we need only consider an arbitrary subsequence, and use the fact that the original sequence converges to finish things up. Then we need to prove if every subsequence converges to the same limit that the original sequence does as well. This is trivial because every sequence is a subsequence of itself.

#realanalysis #math

★DONATE★

Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!

Follow Wrath of Math on...

Рекомендации по теме

Комментарии

You are literally the best analysis teacher around. So simple, direct and well-explained!
Thank you!!!

ranimahassen

Literally saved my life. I've been watching your Real Analysis playlist in preparation for my exam tomorrow. Thank you so much for the videos!! Very helpful.

chisae_

Imagine the difficulty of learning this first handed with English being your second language, it's like listening to a puzzle.

michaelyu

You have some of the best videos on analysis. Every theorem follows a motivating example; every result is presented in the right order with enough justification. If you write a book i’ll pre-order instantly.

Btw, at 2x speed you sound like Jesse Eisenberg

farhanniazi

I can’t visualise the part where k> N1 then k> N is assumed. Isnt N1 < N. theoretically, k< N

sambitgarai

Almost got lost in those notations. Thanks a lot for clarification.

nonentity

Very nice :) !
Is this the Bolzano - wierstrass theorem?

ThePhysicsMathsWizard

7:13 loool that´s a great little proof

manuelkarner

What stops us from taking finite subsequences, can't subsequences be finite? If not can you please point me to some resource mentioning the same, else if they can be finite how does this proof follow for finite subsequences.

vaibhavoutat

does anybody know what's the name of the song at the end?, i really liked the video by the way :)

abrilarellano

Im so confused. If the sequence (a_n) converges to a then there exists some N in the naturals s.t. when n > N |a_n - a| < epsilon. Ok I get that, thats simple. But how does this imply every subsequence converges to a? If I take the first two values in the original sequence as my new subsequence for example (or any subsequence thats indices are less then N)?

kennethnavarro

not to nitpick but ank need not be an infinite sequence or even have terms with indices bigger than K, so what you showed doesnt prove what you set out to prove. I guess I am nitpicking but its important to note.

kushagrasinghal

This is the "freshman's proof" - can you come up with a proof that involves the Choice Function?

NorceCodine

Sequence Converges iff Every Subsequences Converge to the Same Limit | Real Analysis

Sequence Converges iff Every Subsequences Converge to the Same Limit | Real Analysis

A Sequence Converges if and only if every Subsequence Converges Proof | Maths |Mad Teacher

Mathematics: Prove: If a sequence converges, then every subsequence converges to the same limit.

Definition /examples of subsequence, Sequence converges iff its every subsequence converges. Lec-42

A sequence converges to limit l iff if each of its subsequence converges to limit l.

A Sequence Converges if and only if Every Subsequence Converges|Sequence And Series|Real Analysis

Prove: 𝑋𝑛→𝑋 in probability iff for every subseq 𝑋𝑛(𝑚) there’s a further subseq𝑋𝑛(𝑚𝑘)→𝑋 almost surely...

Monotone Sequence with Convergent Subsequence Converges | Real Analysis

Math 131 Fall 2018 102918 Subsequences

Prove Sequence Diverges with Subsequences | Real Analysis

46 Subsequences of convergent sequences part 1

All Subsequences Point to L if...

Every subsequence of convergent sequence converges to same limit.

Proof: Sequence is Cauchy if and only if it Converges | Real Analysis

Sequence (1^n) Diverges using Subsequences | Real Analysis

If Sequence Diverges to Infinity then so do Subsequences | Real Analysis

Subsequence of convergent sequence is convergent and converges to same limit| PROOF

Calculus - Lecture 8 - Subsequences

Sub sequence of a Sequence | Definition | Theorem of sub sequence | Real Analysis | Subsequence

1.4 Subsequences and Monotone Sequences

An Important Fact about Subsequences | Real Analysis

Sequences (Real Analysis) | Subsequences | SE #3 | Sequence {an} exists iff a2n, a2n+1 & a3n exi...

Cauchy sequence has a Convergent subsequence

A sequence of real numbers converges if and only if it is a Cauchy Sequence