filmov
tv
Proof: Sequence 1/sqrt(n) Converges to 0 | Real Analysis

Показать описание
We will prove the sequence 1/sqrt(n) converges to 0. In other words, we're proving that the limit of 1/sqrt(n) as n approaches infinity is 0. We use the epsilon definition of a convergent sequence and the proof is straightforward, following the typical form of a convergent sequence proof.
★DONATE★
Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!
Follow Wrath of Math on...
★DONATE★
Thanks to Robert Rennie and Barbara Sharrock for their generous support on Patreon!
Follow Wrath of Math on...
Proof: Sequence 1/sqrt(n) Converges to 0 | Real Analysis
Proof: Sequence {sqrt(n+1)-sqrt(n)} Converges to 0 | Real Analysis Exercises
Proof: Sequence 1/n Converges to 0 | Real Analysis Exercises
How to Prove a Sequence Converges Example with 1/sqrt(n)
Proof for Square Root of Convergent Sequence | Real Analysis Exercises
Proof: Sequence (n+1)/n Converges to 1 | Real Analysis
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
sqrt(n+1)-sqrt(n) | Limits involving root | Sequence and Limits | Analysis | Math2Go
The nth root of n converges to 1
Definition of the Limit of a Sequence | Real Analysis
an = sqrt(n)/(1 + sqrt(n)) Determine whether the sequence converges or diverges
Proof: lim (-1)^n doesn't converge
How to Prove the Squence a_n = sin(n)/sqrt(n) Converges using the Squeeze Theorem
Proving Sequence Convergence
Determine if the Sequence a_n = n/(1 + sqrt(n)) Converges or Diverges #shorts
How to Prove the Sequence a_n = sin(2n)/(1 + sqrt(n)) Convers with the Squeeze Theorem
Determine if series is convergent or divergent {(sqrt(n+1)- sqrt(n-1))/n}.
Proof: Sequence (-1)^n Diverges | Real Analysis
The nth root of c converges to 1
Does if the Sequence Converge or Diverge a_n = sqrt(n)/(1 + sqrt(n)) #shorts
Series 1/sqrt(n+1) converges or diverges? | Maths |Mad Teacher
Real Analysis: Sequence - L 11 ( Prove that nth root of n converges to 1 ) || IIT-JAM, CSIR-NET ||
Determine if series is absolutely, conditionally convergent or divergent (-1)^n/(1+ sqrt(n))
Prove that the sequence √(n+1)-√n is monotonic, bounded and convergent|| Real analysis
Комментарии
 0:07:13
0:07:13
 0:11:06
0:11:06
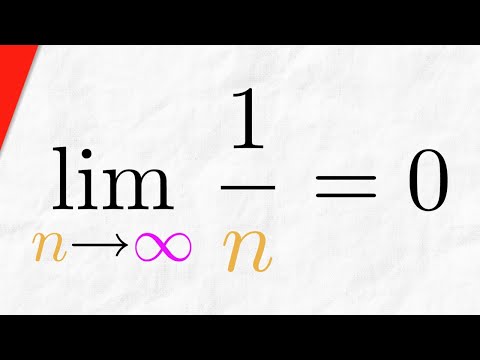 0:06:48
0:06:48
 0:03:58
0:03:58
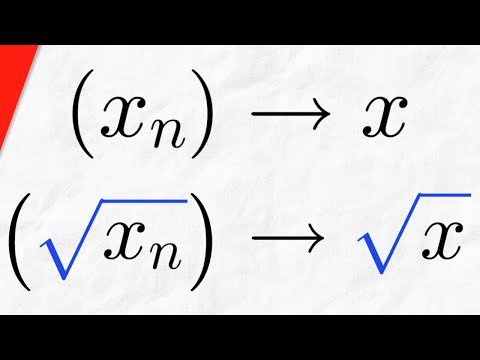 0:12:54
0:12:54
 0:06:43
0:06:43
 0:06:53
0:06:53
 0:04:01
0:04:01
 0:10:14
0:10:14
 0:13:59
0:13:59
 0:01:20
0:01:20
 0:05:37
0:05:37
 0:02:28
0:02:28
 0:06:34
0:06:34
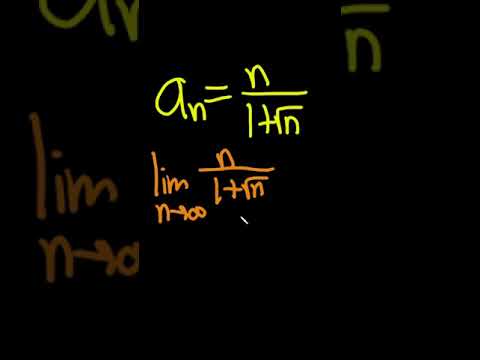 0:00:45
0:00:45
 0:02:21
0:02:21
 0:05:07
0:05:07
 0:13:07
0:13:07
 0:22:13
0:22:13
 0:00:46
0:00:46
 0:04:03
0:04:03
 0:22:18
0:22:18
 0:04:09
0:04:09
 0:09:51
0:09:51