filmov
tv
Differential Equations: Direction Fields

Показать описание
As explained in my earlier videos, most differential equations can't be solved explicitly which thus forces us to find different ways of estimating the solution; and one of those is in the concept of direction fields. For differential equations of the form y' = F(x, y), a direction field (or slope field) is any number of points in which the slope of the line segment near that point is plotted out. This allows us to get a general idea of the shape of the curve. Direction fields are very useful to visually see the solution of a differential equation without actually having to know the precise solution. This is a very important concept to understand so make sure to watch this video!
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
Slope Fields | Calculus
The Geometric Meaning of Differential Equations // Slope Fields, Integral Curves & Isoclines
Creating a slope field | First order differential equations | Khan Academy
Differential Equations: Direction Fields: Example 1
Introduction to Slope Fields (Differential Equations 9)
Differential equation from slope field | First order differential equations | Khan Academy
Drawing Slope Fields from Differential Equations - Calculus 2
Sketching direction fields (KristaKingMath)
Quantum Field Theory Made Easier 4 | Picturing Quantum Symmetries!
Direction Field Concept to Sketch Graph of Solution of Differential Equation
Differential equations, a tourist's guide | DE1
Matching Slope Fields with Differential Equations
Introduction to Slope Fields
Differential Equation - Introduction (10 of 15) What Are Slope Fields and Solution Curves - 1?
Differential Equations Slope Fields Interpretation IB AB AP Calculus - EDEXCEL - GCSE - SAT
Slope field to visualize solutions | First order differential equations | Khan Academy
Direction Fields (Differential Equations)
Slope Fields (First-Order Differential Equations)
Sketch the slope field of the differential equation
Applications of Slope Fields (Differential Equations 10)
Matching Slope Fields and Differential Equations
Differential Equations: Direction Fields Introduction
Differential Equations Direction Fields: Example 2: Electric Circuit
Differential Equations: Direction Fields
Комментарии
 0:21:12
0:21:12
 0:09:52
0:09:52
 0:05:51
0:05:51
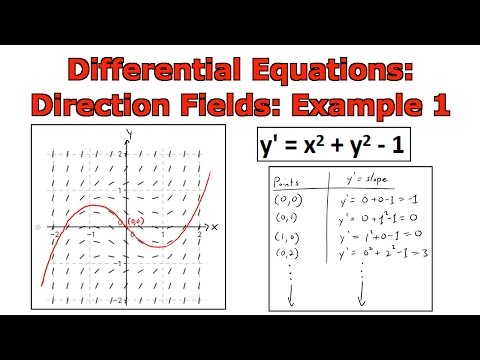 0:05:47
0:05:47
 0:34:18
0:34:18
 0:06:10
0:06:10
 0:08:01
0:08:01
 0:08:37
0:08:37
 0:28:41
0:28:41
 0:08:29
0:08:29
 0:27:16
0:27:16
 0:08:39
0:08:39
 0:09:35
0:09:35
 0:04:38
0:04:38
 0:45:26
0:45:26
 0:06:55
0:06:55
 0:11:36
0:11:36
 0:12:11
0:12:11
 0:04:00
0:04:00
 0:38:42
0:38:42
 0:05:46
0:05:46
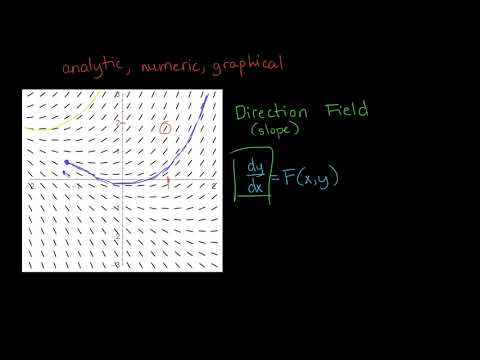 0:06:36
0:06:36
 0:14:46
0:14:46
 0:09:33
0:09:33