filmov
tv
Slope Fields (First-Order Differential Equations)

Показать описание
This ordinary differential equations video explains slope fields, isoclines, autonomous equations, equilibrium points, phase lines, and stability of constant solutions. We begin with what a slope field (or direction field) is and show several examples of what these look like for a first-order differential equation. We show what an isocline is in a slope field--a region of the field with the same slope. We also describe what an autonomous differential equation is, how to find its critical points (or equilibrium points), and how these relate to the constant solutions for the differential equation. We introduce a one-dimensional phase portrait for the slope fields, and show examples of the different types of critical points: asymptotically stable (attractor), unstable (repeller), and semi-stable.
0:00 What is a slope field?
0:56 Example 1
1:40 Example with an isocline
2:30 Autonomous equations and critical points
3:51 Exponential change slope field
4:48 Logistic growth slope field
6:10 Stability of equilibrium points
8:50 Phase portraits
0:00 What is a slope field?
0:56 Example 1
1:40 Example with an isocline
2:30 Autonomous equations and critical points
3:51 Exponential change slope field
4:48 Logistic growth slope field
6:10 Stability of equilibrium points
8:50 Phase portraits
Differential equation from slope field | First order differential equations | Khan Academy
Creating a slope field | First order differential equations | Khan Academy
Slope Fields | Calculus
Slope field to visualize solutions | First order differential equations | Khan Academy
The Geometric Meaning of Differential Equations // Slope Fields, Integral Curves & Isoclines
Interpret a first order differential equation as a slope field
Slope Field of First Order Differential Equations
ODE | Slope fields
Can we design transistors one atom at a time?
Introduction to Slope Fields (Differential Equations 9)
Slope Fields (First-Order Differential Equations)
Slope fields for first-order ordinary differential equations
First Order Linear Differential Equations
Introduction to Slope Fields
Slope Fields and Euler's Method Explained (with examples)
The slope fields of first order differential equations
Differential equations, a tourist's guide | DE1
Solving a First-Order Differential Eq with a Slope Field Comparison ❖ Calculus 1
Differential Equations: Direction Fields: Example 1
Sketch the slope field of the differential equation
Slope Fields of Autonomous Differential Equations
Differential Equation - Introduction (11 of 15) What Are Slope Fields and Solution Curves - 2?
Matching Slope Fields with Differential Equations
Differential Equation - Introduction (10 of 15) What Are Slope Fields and Solution Curves - 1?
Комментарии
 0:06:10
0:06:10
 0:05:51
0:05:51
 0:21:12
0:21:12
 0:06:55
0:06:55
 0:09:52
0:09:52
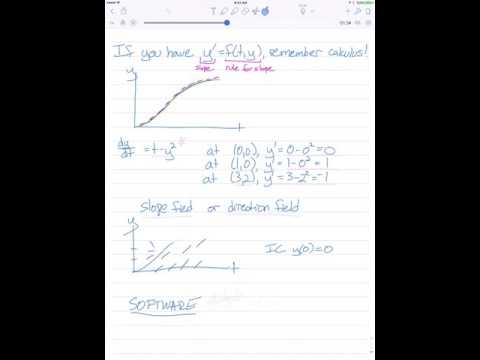 0:03:41
0:03:41
 0:07:37
0:07:37
 0:04:40
0:04:40
 0:59:40
0:59:40
 0:34:18
0:34:18
 0:12:11
0:12:11
 0:34:12
0:34:12
 0:22:28
0:22:28
 0:09:35
0:09:35
 0:12:14
0:12:14
 0:19:18
0:19:18
 0:27:16
0:27:16
 0:06:42
0:06:42
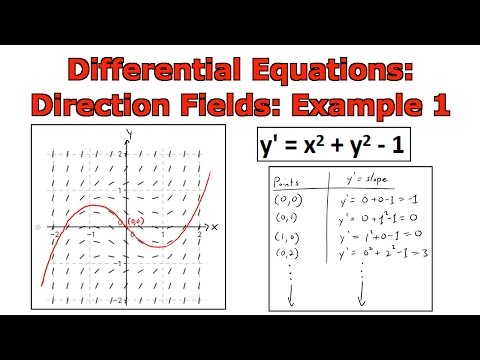 0:05:47
0:05:47
 0:04:00
0:04:00
 0:08:43
0:08:43
 0:05:19
0:05:19
 0:08:39
0:08:39
 0:04:38
0:04:38