filmov
tv
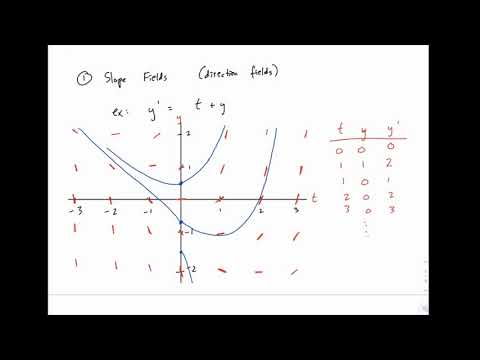
Introduction to Slope Fields (Differential Equations 9)

Показать описание
A constructive approach to Slope Fields and how they work. Individual exploration with a Computer Graphing application is highly recommended.
Slope Fields | Calculus
Introduction to Slope Fields (Differential Equations 9)
Creating a slope field | First order differential equations | Khan Academy
Introduction to Slope Fields
The Geometric Meaning of Differential Equations // Slope Fields, Integral Curves & Isoclines
Slope field to visualize solutions | First order differential equations | Khan Academy
Differential Equation - Introduction (10 of 15) What Are Slope Fields and Solution Curves - 1?
Differential equation from slope field | First order differential equations | Khan Academy
Differential Equation - Introduction (11 of 15) What Are Slope Fields and Solution Curves - 2?
Differential equations, a tourist's guide | DE1
Drawing Slope Fields from Differential Equations - Calculus 2
Introduction to Slope Fields
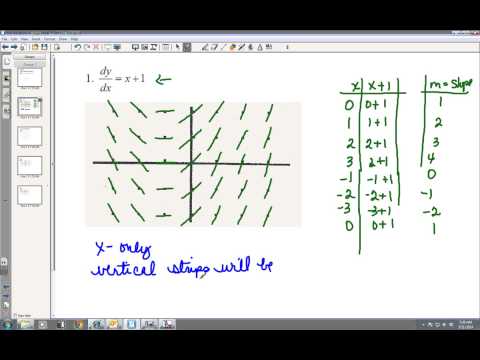
Sketch the slope field of the differential equation
Differential Equations - Intro Video - Slope Fields
Introduction to Slope Fields in Colaboratory
Matching Slope Fields with Differential Equations
Calculus 2: 72 - Introduction to slope fields
Differential Equations and Slope Fields
Introduction to Slope Fields and Differential Equations
Isoclines: A Way to Analyze Slope Fields
Introduction to slope fields
Introduction to Slope Fields
Applications of Slope Fields (Differential Equations 10)
Intro to Direction Fields
Комментарии
 0:21:12
0:21:12
 0:34:18
0:34:18
 0:05:51
0:05:51
 0:09:35
0:09:35
 0:09:52
0:09:52
 0:06:55
0:06:55
 0:04:38
0:04:38
 0:06:10
0:06:10
 0:05:19
0:05:19
 0:27:16
0:27:16
 0:08:01
0:08:01
 0:11:23
0:11:23
 0:04:00
0:04:00
 0:03:57
0:03:57
 0:16:52
0:16:52
 0:08:39
0:08:39
 0:10:52
0:10:52
 0:11:24
0:11:24
 0:38:28
0:38:28
 0:08:14
0:08:14
 0:16:15
0:16:15
 0:10:32
0:10:32
 0:38:42
0:38:42
 0:05:42
0:05:42