filmov
tv
Differential Equations: Direction Fields: Example 1
Показать описание
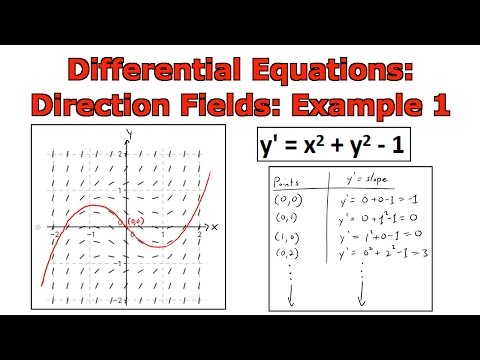
In this video I go over an example on how to go about generating a direction field as well as using it to draw a particular solution. The differential equation used is y' = x^2 + y^2 - 1 and a particular solution is graphed that passes through the origin (0, 0). This is a pretty simple but useful video in showing how we can estimate a solution to the differential equation without knowing the actual formula for the solution.
Related Videos:
------------------------------------------------------
Related Videos:
------------------------------------------------------
0:21:12
Slope Fields | Calculus
0:05:47
Differential Equations: Direction Fields: Example 1
0:08:37
Sketching direction fields (KristaKingMath)
0:05:51
Creating a slope field | First order differential equations | Khan Academy
0:09:52
The Geometric Meaning of Differential Equations // Slope Fields, Integral Curves & Isoclines
0:06:10
Differential equation from slope field | First order differential equations | Khan Academy
0:34:18
Introduction to Slope Fields (Differential Equations 9)
0:08:01
Drawing Slope Fields from Differential Equations - Calculus 2
0:08:48
Maxwell's 4th Equation Explained: Integral Form and Differential Form/Point Form
0:09:35
Introduction to Slope Fields
0:06:55
Slope field to visualize solutions | First order differential equations | Khan Academy
0:08:39
Matching Slope Fields with Differential Equations
0:07:07
Direction Field Sketch Graph of f'=x+y Solution of Difference Equation
0:11:36
Direction Fields (Differential Equations)
0:04:38
Differential Equation - Introduction (10 of 15) What Are Slope Fields and Solution Curves - 1?
0:13:58
Differential Equations: Quick and Easy Way to Create Direction Fields
0:04:00
Sketch the slope field of the differential equation
0:08:29
Direction Field Concept to Sketch Graph of Solution of Differential Equation
0:06:36
Differential Equations: Direction Fields Introduction
0:14:46
Differential Equations Direction Fields: Example 2: Electric Circuit
0:03:54
Differential Equations - 3 - EXAMPLE - Slope Field and Solution for y'=xy
0:11:15
Differential Equations - 2 - Slope Fields
0:08:14
Isoclines: A Way to Analyze Slope Fields
0:05:54
ODE | Phase diagrams
Комментарии