filmov
tv
Solving a Cubic System for Real Solutions

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#Algebra #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving a Cubic System for Real Solutions
Solving a Cubic System
Solving a cubic system for real solutions
Solving a cubic system
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
solving a cubic equation by completing the cube
Solving a Nice Cubic System in Two Ways
Solving a Cubic Polynomial System in Two Ways
Solving A Nice Cubic System in Two Ways
Solving a cubic equation
Solving A Cubic System #algebra #polynomials
A cubic system of equations
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Classwiz How-To: Solving a Cubic Equation
Solving a Cubic System in a Non-polynomial Way
Can You Factor and Solve This Cubic Equation In Under a Minute? - Simple Math Trick
Solving a Cubic equation Using an Algebraic Trick
How to Solve Advanced Cubic Equations: Easy-to-Understand Explanation
Solving a Cubic Polynomial in Two Ways
Solving A Cubic System | Problem 335
How to Solve Cubic Equations using the Total Sum Method
How to prove the cubic formula (from scratch)
Solve Cubic Equations: Fast Alternative Method
Solving An Interesting Cubic System for x + y + z
Комментарии
 0:09:15
0:09:15
 0:14:14
0:14:14
 0:09:15
0:09:15
 0:14:14
0:14:14
 0:10:52
0:10:52
 0:07:28
0:07:28
 0:09:13
0:09:13
 0:09:09
0:09:09
 0:09:41
0:09:41
 0:07:26
0:07:26
 0:08:41
0:08:41
 0:13:25
0:13:25
 0:07:18
0:07:18
 0:03:14
0:03:14
 0:09:29
0:09:29
 0:08:46
0:08:46
 0:11:45
0:11:45
 0:11:25
0:11:25
 0:09:55
0:09:55
 0:10:14
0:10:14
 0:06:57
0:06:57
 0:40:16
0:40:16
 0:08:52
0:08:52
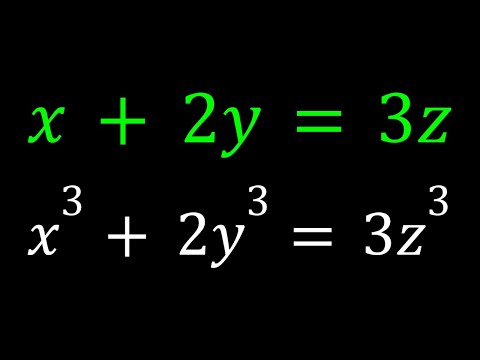 0:09:25
0:09:25