filmov
tv
Solving a Cubic Polynomial System in Two Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialSystems
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialSystems
PLAYLISTS 🎵 :
Solving a Cubic Polynomial System in Two Ways
A Cubic Polynomial System
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solving a Cubic Polynomial in Two Ways
Solve the Nonlinear System: A Cubic Polynomial and a Line
Solving Polynomial Equations By Factoring and Using Synthetic Division
Solve a Cubic Polynomial Function | Maths | Leaving Cert Maths |
Solving a Cubic System in a Non-polynomial Way
Factoring a cubic polynomial
Factoring a Cubic Polynomial (Long Division)
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Find cubic polynomial through 4 points
Solving a Cubic equation Using an Algebraic Trick
How To Solve Cubic Polynomial Equations
Factor Cubic Polynomial with Fractions
How to Solve Advanced Cubic Equations: Easy-to-Understand Explanation
How to solve cubic polynomial equations by factoring and division GCSE Precalculus
Solving system of equation with cubic polynomial.
Solving a Polynomial System of Equations
Factor Cubic Polynomial
Germany Math Olympiad, a system of cubic equations
Solving A Cubic | Polynomial Equations | All 3 Roots! #maths
Find Complex Roots of a Cubic Equation z^3 - 3z^2 + z + 5 = 0
5 simple unsolvable equations
Комментарии
 0:09:09
0:09:09
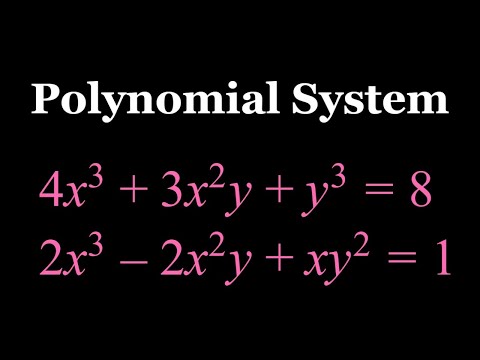 0:10:31
0:10:31
 0:10:52
0:10:52
 0:09:55
0:09:55
 0:08:17
0:08:17
 0:14:19
0:14:19
 0:02:32
0:02:32
 0:09:29
0:09:29
 0:06:30
0:06:30
 0:08:58
0:08:58
 0:07:18
0:07:18
 0:11:20
0:11:20
 0:11:45
0:11:45
 0:13:58
0:13:58
 0:07:18
0:07:18
 0:11:25
0:11:25
 0:13:19
0:13:19
 0:06:17
0:06:17
 0:11:00
0:11:00
 0:04:58
0:04:58
 0:11:36
0:11:36
 0:02:08
0:02:08
 0:05:54
0:05:54
 0:00:50
0:00:50