filmov
tv
Solving a Cubic Polynomial in Two Ways
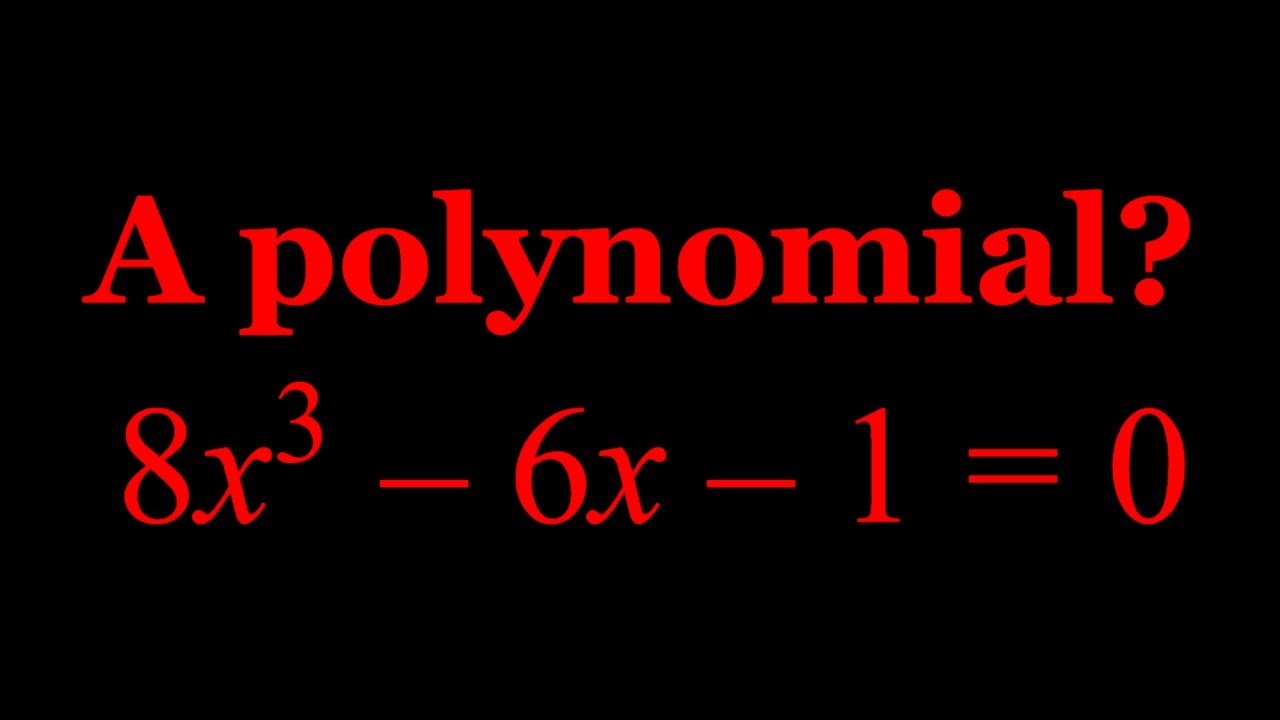
Показать описание
This video is about solving a Polynomial Equation
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
EXPLORE:
Simple way to solve a cubic equation
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solving a simple cubic equation. A trick you should know!
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solving Polynomial Equations By Factoring and Using Synthetic Division
Solve any Cubic Equations | Cardano's Method |
Factorising cubic functions: The kx method
so you want to see the cubic formula
The Cubic Formula - Cardanos Method #SoMEpi
Factorise Cubic Equation Grade 12: Introduction
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving Simple Cubic Equations
Solving a Cubic Polynomial in Two Ways
solving equations but they get increasingly awesome
Exam Problem: Cubic Polynomial w/ 1 Real Root
Solve a Cubic Polynomial Function | Maths | Leaving Cert Maths |
How to factor a cubic function
Factoring a Cubic Polynomial (Long Division)
How to factor a polynomial using the difference of two cubes
Solving Cubic Equations (factoring)
Can You Factor and Solve This Cubic Equation In Under a Minute? - Simple Math Trick
Solving a Cubic Polynomial System in Two Ways
Find cubic polynomial through 4 points
Комментарии
 0:04:56
0:04:56
 0:10:52
0:10:52
 0:06:41
0:06:41
 0:36:58
0:36:58
 0:14:19
0:14:19
 0:04:20
0:04:20
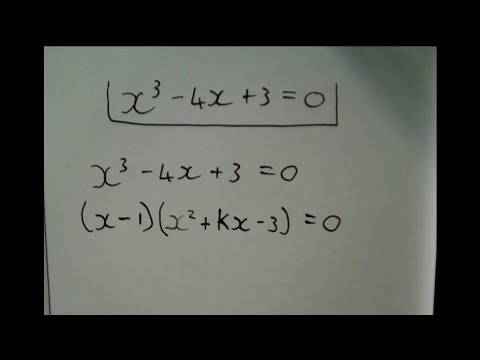 0:10:22
0:10:22
 0:40:16
0:40:16
 0:00:28
0:00:28
 0:06:17
0:06:17
 0:12:06
0:12:06
 0:07:18
0:07:18
 0:09:13
0:09:13
 0:09:55
0:09:55
 0:10:44
0:10:44
 0:09:55
0:09:55
 0:02:32
0:02:32
 0:04:45
0:04:45
 0:08:58
0:08:58
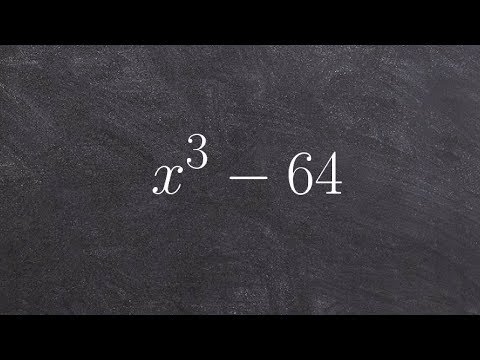 0:02:21
0:02:21
 0:03:32
0:03:32
 0:08:46
0:08:46
 0:09:09
0:09:09
 0:11:20
0:11:20