filmov
tv
Solving a Cubic equation Using an Algebraic Trick

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #PolynomialEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
Simple way to solve a cubic equation
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solve any Cubic Equations | Cardano's Method |
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving Cubic Equations (factoring)
Solving a Cubic equation Using an Algebraic Trick
solving a cubic equation by completing the cube
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Finding C. F. for the Linear Homogeneous PDE with Constant Coefficients, Unit 1 - 21MAB201T
How To ACTUALLY Solve a Cubic Equation using Trigonometry
How to Solve Advanced Cubic Equations: Easy-to-Understand Explanation
Classwiz How-To: Solving a Cubic Equation
Solving a simple cubic equation. A trick you should know!
Factorise Cubic Equation Grade 12: Introduction
How to Solve a Rubik’s Cube in 4 Moves
How to solve cubic equation by Casio calculator
Solve Cubic Equations - Total Sum Method
Factorising cubic functions: The kx method
Find Factors and Solve Cubic Equations in Less Than ONE Minute! - Leading Coefficient Is Not One
Can You Solve this Cubic Equation in 1 Minute? | Quick & Simple Explanation
so you want to see the cubic formula
Solve Cubic Equations - Synthetic Division Method
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Solving Simple Cubic Equations
Комментарии
 0:04:56
0:04:56
 0:10:52
0:10:52
 0:04:20
0:04:20
 0:07:18
0:07:18
 0:03:32
0:03:32
 0:11:45
0:11:45
 0:07:28
0:07:28
 0:36:58
0:36:58
 0:14:28
0:14:28
 0:14:58
0:14:58
 0:11:25
0:11:25
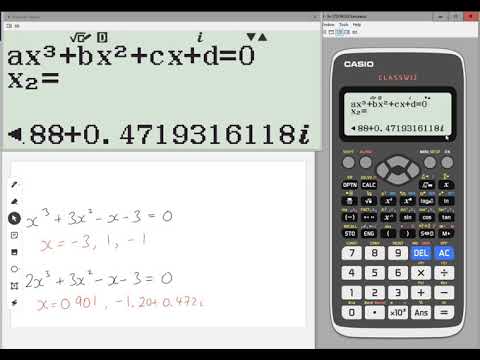 0:03:14
0:03:14
 0:06:41
0:06:41
 0:06:17
0:06:17
 0:01:15
0:01:15
 0:01:40
0:01:40
 0:09:51
0:09:51
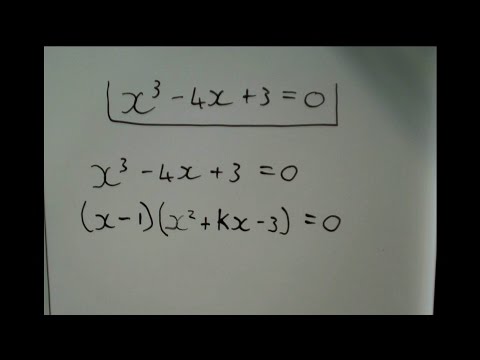 0:10:22
0:10:22
 0:09:10
0:09:10
 0:02:52
0:02:52
 0:40:16
0:40:16
 0:09:30
0:09:30
 0:12:06
0:12:06
 0:09:13
0:09:13