filmov
tv
Solving a cubic equation
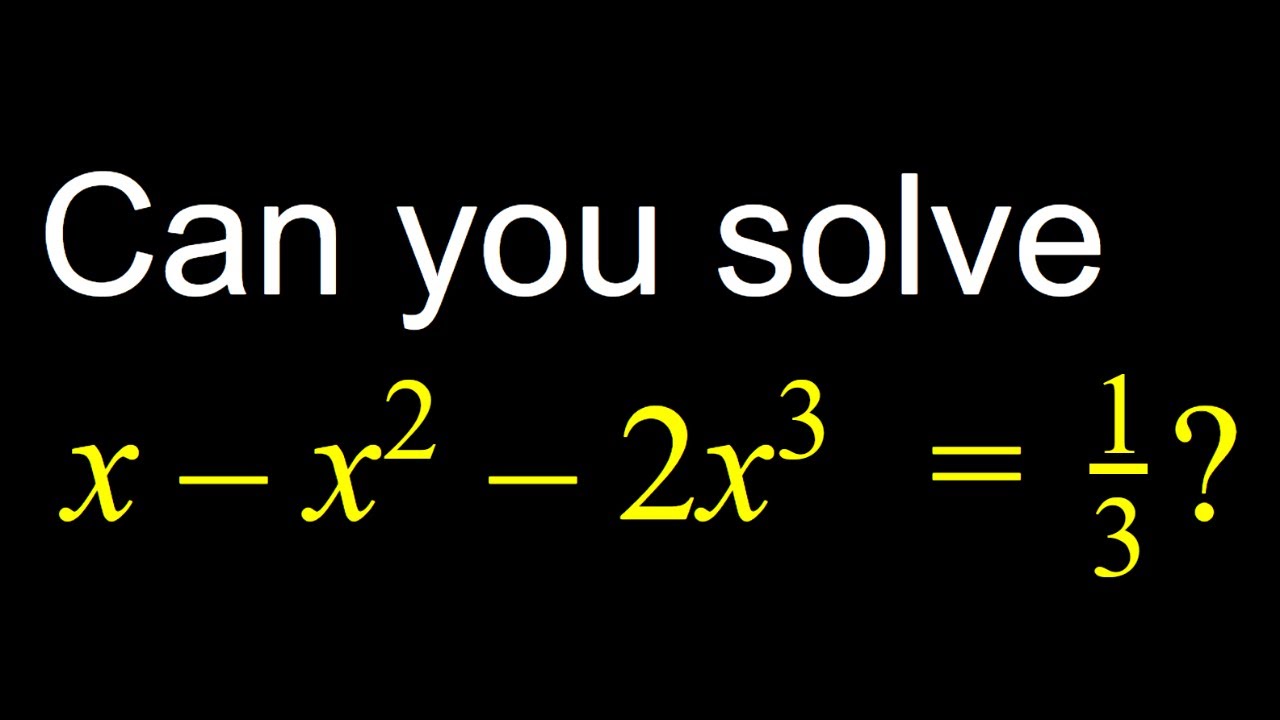
Показать описание
This video is about a cubic equation
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#ChallengingMathProblems
Send me a tweet at @SyberMath if you want to share a picture of your solution/ideas and comment here with the link to the tweet.
#ChallengingMathProblems
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Simple way to solve a cubic equation
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solve any Cubic Equations | Cardano's Method |
Solving a simple cubic equation. A trick you should know!
solving a cubic equation by completing the cube
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving Cubic Equations (factoring)
Algebraic Identities - Concepts & Examples (Part 1) Polynomials | Class 9 Maths Chapter 2 #cbse
so you want to see the cubic formula
Solving Simple Cubic Equations
Solving a Cubic equation Using an Algebraic Trick
How to Solve Advanced Cubic Equations: Easy-to-Understand Explanation
CUBIC EQUATION FACTORIZATION SHORTCUT/ SOLVING CUBIC EQUATIONS IN 10 SECONDS/ Math Tricks.
Factorise Cubic Equation Grade 12: Introduction
How To Solve Cubic Equations
Factorising cubic functions: The kx method
Solve Cubic Equations - Total Sum Method
Solve Cubic Equations: Fast Alternative Method
Solving General Cubic Equations
Cubic Formula for Depressed Cubic
How To ACTUALLY Solve a Cubic Equation using Trigonometry
Find Factors and Solve Cubic Equations in Less Than ONE Minute! - Leading Coefficient Is Not One
The Cubic Formula: Roots of the General Cubic Equation
Комментарии
 0:10:52
0:10:52
 0:04:56
0:04:56
 0:36:58
0:36:58
 0:04:20
0:04:20
 0:06:41
0:06:41
 0:07:28
0:07:28
 0:07:18
0:07:18
 0:03:32
0:03:32
 0:50:06
0:50:06
 0:40:16
0:40:16
 0:09:13
0:09:13
 0:11:45
0:11:45
 0:11:25
0:11:25
 0:12:06
0:12:06
 0:06:17
0:06:17
 0:09:29
0:09:29
 0:10:22
0:10:22
 0:09:51
0:09:51
 0:08:52
0:08:52
 0:08:59
0:08:59
 0:14:24
0:14:24
 0:14:58
0:14:58
 0:09:10
0:09:10
 0:04:50
0:04:50