filmov
tv
Solving A Cubic System #algebra #polynomials

Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#algebra #polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving a Cubic System
Solving a cubic system
Solving a Cubic System for Real Solutions
How to Solve Advanced Cubic Equations: Step-by-Step Tutorial
Solving a cubic equation
Solving A Cubic System #algebra #polynomials
solving a cubic equation by completing the cube
Solving a cubic system for real solutions
Calculus NCEA Level 2 in 15 hours | Part 3
Solving a Nice Cubic System in Two Ways
Solving a Cubic equation Using an Algebraic Trick
Solving a Cubic Polynomial System in Two Ways
A cubic system of equations
Factor and Solve Cubic Equations in Less Than One Minute! - Super Simple Trick
Solving a Cubic System in a Non-polynomial Way
Solving a cubic equation with irrational coefficients. A radical challenge in algebra.
Solving a cubic equation with an irrational root
Can You Factor and Solve This Cubic Equation In Under a Minute? - Simple Math Trick
How to Solve Cubic Equations using the Total Sum Method
A Nice Cubic Equation - Number Theory | Advanced Math
Classwiz How-To: Solving a Cubic Equation
Can you solve this cubic equation by factoring?
How to Solve Cubic Equations: Quick Factoring Method
Germany Math Olympiad, a system of cubic equations
Комментарии
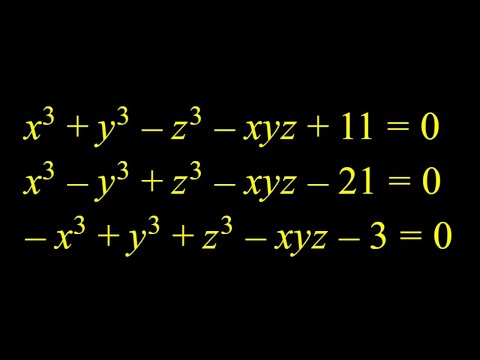 0:14:14
0:14:14
 0:14:14
0:14:14
 0:09:15
0:09:15
 0:10:52
0:10:52
 0:07:26
0:07:26
 0:08:41
0:08:41
 0:07:28
0:07:28
 0:09:15
0:09:15
 1:08:10
1:08:10
 0:09:13
0:09:13
 0:11:45
0:11:45
 0:09:09
0:09:09
 0:13:25
0:13:25
 0:07:18
0:07:18
 0:09:29
0:09:29
 0:06:36
0:06:36
 0:16:23
0:16:23
 0:08:46
0:08:46
 0:06:57
0:06:57
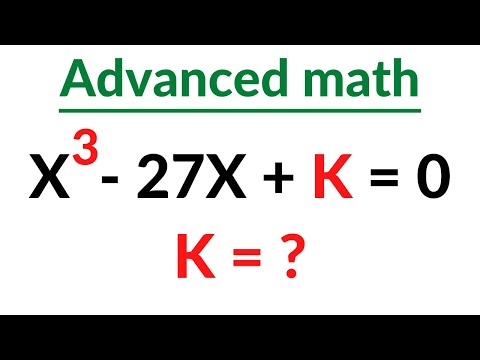 0:08:36
0:08:36
 0:03:14
0:03:14
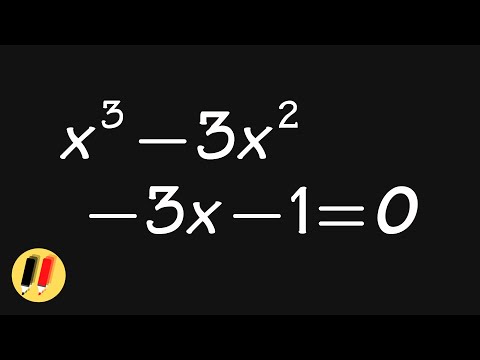 0:00:59
0:00:59
 0:07:10
0:07:10
 0:11:36
0:11:36