Proving Euler's Identity FAST

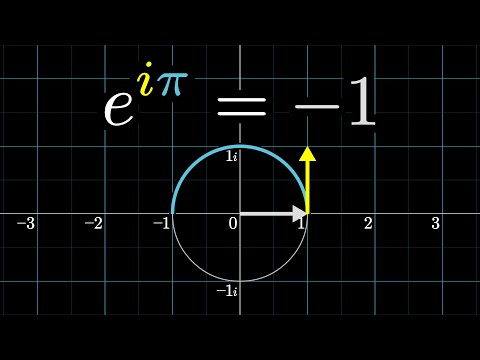
Euler's identity is very useful for dealing with complex numbers. Let's prove it in less than two minutes!

New math videos every Monday and Friday. Subscribe to make sure you see them!

[ronak]

In a few years: Proving Fermat's last theorem fast.





In few decades: Proving Riemann Hypothesis fast.

[michaelgeorgievski]

This is so good it almost looks like cheating

[emperorpingusmathchannel]

You can pretty much copy and paste this method for most identities eg:
sin^2(x)+cos^2(x)=1


f(x)= sin^2(x)+cos^2(x)-1
f'(x)=0
f(some arbitrary real number)=0


Boom proof.


What is ironic is that it required more steps than the original heuristic proof using a triangle.

[BluePi]

I would have never thought to do it this way. Great work!

[chirayu_jain]

You did it from derivative. Never thought of that 🤔🤔🤔. Nice video

[EpicMathTime]

I've never seen it done this way.

[w.nickel]

Nice method. It can be used to prove many other identities, e.g. sin^2 + cos^2 = 1.

[xxxprawn]

Fantastic video, I’ve been wondering about that proof for soooo long, and I have to admit the way you presented it using calculus is genius, thanks!

[Tengdbuddy]

A wild Euler appears. Mu uses speed boost. It's super effective.

[jfcrow]

Bravo I wish my math teacher knew that when I was in college 30 years ago.

[brendanchamberlain]

Can you explain how you knew that e^ix and cos(x)+isin(x) are differentiable? Wouldn't having an imaginary number in there mess things up? Also, is there a proof of the rule that shows (e^u)' = ze^u, u=zx, where Im(z) is nonzero? I have only seen this derivative rule proven for real numbers. I haven't taken complex analysis or anything, so I apologize if the answer is obvious. Thank you!

[EricTai]

Easy to understand and very fast proof

[michaelholm]

One issue in your video: When you say that we don't really care what the denominator is. If the denominator also turns out to be zero, you're in trouble and your approach is broken.

[Invalid]

One thing is bothering me with this proof:
We showed that y(t) = c everything is good up to this point.
Then we chose t = 0 and got Euler formula as we wanted but what if we chose another value?
E.g. let t = π/2 or t = π
If t = π/2: c = ... = -i*(e^(iπ/2))
If t = π: c = ... = -e^(iπ)
So why do we prefer t = 0 over any other value?
🤔

Have I missed something?

[VibingMath]

I have a feeling that you do this intentionally for other future videos 😆

[zakariaelghaouti]

Very fast😂😂😂😂 I liked this video. Thanks

[AsadullahJamalFaizi]

But I can't ever thought that It can be solve from derivative AWESOME mu prime math

[willnewman]

What is you definiton of the function e^t?

[swapnilghosal]

A clever one!!! I must appreciate your efforts but not satisfied by the fact that you can differentiate complex functions, as per I know calculus is all about real analysis. I apologize, if I say something wrong. Thank you.

[MarkMcDaniel]

Instructor gives you kudos for a correct answer, but only gives you 3/5 points for not formatting the exact way they like it.