filmov
tv
Deriving Black Scholes

Показать описание
In this video, we derive the famous Black-Scholes Equation, the basis of all option pricing. I tried not to skip any steps, and tried to explain everything I was doing, so the derivation ought to be easy to follow. Let me know if I failed!
For this video, we need to know Ito's Lemma, and we need to work with Geometric Brownian motion, so it is highly advised that you go through those videos first!
Ito's Lemma:
Geometric Brownian Motion:
If you learn something, please click the Like button.
If you want to keep learning, go ahead an subscribe!
For this video, we need to know Ito's Lemma, and we need to work with Geometric Brownian motion, so it is highly advised that you go through those videos first!
Ito's Lemma:
Geometric Brownian Motion:
If you learn something, please click the Like button.
If you want to keep learning, go ahead an subscribe!
The Easiest Way to Derive the Black-Scholes Model
Introduction to the Black-Scholes formula | Finance & Capital Markets | Khan Academy
Black-Scholes PDE Derivation in 4 minutes
Deriving Black Scholes
Derivation of the Black-Scholes equation
Black Scholes Derivation
Warren Buffett: Black-Scholes Formula Is Total Nonsense
A simple derivation of the Black-Scholes equation
Deriving the Black Scholes Call Formula
Deriving the Black-Scholes Pricing Equation
19. Black-Scholes Formula, Risk-neutral Valuation
Derivation of Black-Scholes Equation |FULL|
The Trillion Dollar Equation
Black Scholes Formula explained simply
Deriving Black-Scholes Theorem on Live
Black Scholes Explained - A Mathematical Breakdown
Deriving Black-Scholes Using Ito's Lemma
Black-Scholes Equation (Financial Engineering)
Charlie Munger on Black–Scholes
Measure change approach to the derivation of Black Scholes
Unlocking the Black-Scholes Model: Visualizing the Power of Options Trading in 60 Seconds
The Math of 'The Trillion Dollar Equation'
Derivation of the Black-Scholes PDE
An intuitive explanation the Black Scholes' formula
Комментарии
 0:09:53
0:09:53
 0:10:24
0:10:24
 0:04:30
0:04:30
 0:17:24
0:17:24
 0:15:04
0:15:04
 0:16:55
0:16:55
 0:15:54
0:15:54
 0:27:31
0:27:31
 0:13:34
0:13:34
 0:10:41
0:10:41
 0:49:52
0:49:52
 0:00:12
0:00:12
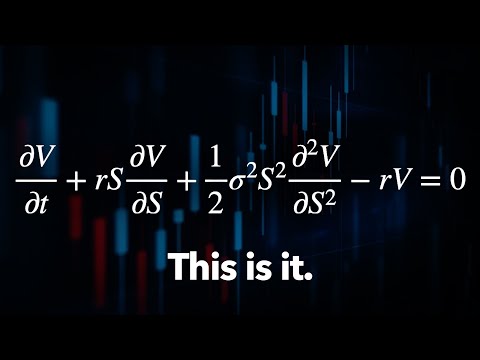 0:31:22
0:31:22
 0:03:40
0:03:40
 0:00:12
0:00:12
 0:14:03
0:14:03
 0:21:06
0:21:06
 0:05:59
0:05:59
 0:00:39
0:00:39
 0:05:44
0:05:44
 0:00:59
0:00:59
 0:30:15
0:30:15
 0:03:58
0:03:58
 0:05:48
0:05:48