filmov
tv
The Math of 'The Trillion Dollar Equation'

Показать описание
Here are my notes from I was a PhD student on this stuff (we were allowed to bring in short notes to the exam)
0:00 The Trillion Dollar Equation
0:18 Veritasium's Example of the Call Option
2:13 The function v(s t) for the value of the option
3:29 Veritasium's Delta hedged portfolio
4:19 Veritasium's slide by derivation
5:24 Derivation of the Black-Scholes equation from scratch
8:26 Change in portfolio value d Pi t
9:47 Approximate changes by derivatives of v a la Taylor series
15:08 Model for the stock price S t Geometric Brownian Motion
19:42 d S t squared is just a dt a la Itos Lemma
25:44 Set delta to di v di s to perfectly hedge
27:23 Equate to the risk free interest rate equation
29:10 But isnt delta a function of time? Why does this work?
The Trillion Dollar Equation
The Math of 'The Trillion Dollar Equation'
The Trillion Dollar FLAW in Financial Market Trading
The Trillion dollar mathematical equation.
man vs machine: 1 TRILLION math problems
Million, Billion, Trillion, Lakhs, Crores?😕 - Part 1 | Fun Math | Don't Memorise
The Simplest Math Problem No One Can Solve - Collatz Conjecture
👉 Million / Billion / Trillion / Arab / Kharab / Nil 🤔 !! #maths #kharab #arab #million #shorts...
Million, Billion, Trillion
One Trillion Dollars (In Seconds) Interesting Math & Money Breakdown
Meaning of Million, Billion,Trillion | Number System #shorts #maths #million #trillion #numbers
#million #billion #trillion #quadrillion#maths#important
Hey siri what’s 1 Trillion to the 10th power…💀#viral #shorts
million billion trillion conversion of number
Compounding example_ $1 in 1776 to over $5 trillion in 2021 #shorts #maths #trillion
1 Million Vs 1 Billion Vs 1 Trillion Vs 1 Quadrillion | What is a Centillion? | Epic Powers of 10
#shorts 😎How Many Zeros Are in All Numbers, Million, Billion, Trillion, Sextillion? #mathematics
Exploring Big Numbers like Billion, Trillion, Decilion. #billion #trillion #googol #math #maths
Doubles Addition Facts Song
NumberBlock from ONE to TRILLION FAST! #shorts #numberblocks #minecraft #trillion #fast
How Many Zero Are In a Trillion!#maths #youtubeshorts #shortsvideo #ytshorts #yt #mathsfact #youtube
What if you had a Trillion Dollars? + more videos | #aumsum #kids #science #education #children
Meaning of Million, Billion, Trillion #shorts #counting
Million Billion Trillion quadrillion... #mathstricks #shorts #basicmaths
Комментарии
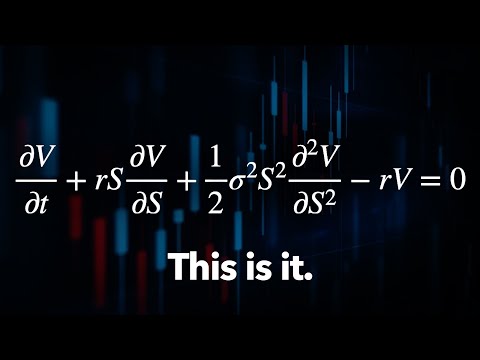 0:31:22
0:31:22
 0:30:15
0:30:15
 0:07:55
0:07:55
 0:06:41
0:06:41
 0:01:01
0:01:01
 0:01:12
0:01:12
 0:22:09
0:22:09
 0:00:39
0:00:39
 0:00:15
0:00:15
 0:00:24
0:00:24
 0:00:33
0:00:33
 0:00:10
0:00:10
 0:00:40
0:00:40
 0:00:05
0:00:05
 0:00:23
0:00:23
 0:09:52
0:09:52
 0:00:49
0:00:49
 0:00:57
0:00:57
 0:01:56
0:01:56
 0:00:22
0:00:22
 0:00:28
0:00:28
 0:05:29
0:05:29
 0:00:05
0:00:05
 0:00:08
0:00:08