filmov
tv
Triangle Inequality of Complex Number

Показать описание
Triangle Inequality of Complex Number states that the absolute value of sum of two complex number is always less than or equal to the sum of individual absolute value of the complex numbers. Absolute value of the complex number represents here the modulus value of the complex number. It is very important concept of complex number algebra.
If we have complex number z & w, then triangle inequality states that
(abs.Z + abs. W ) is greater than abs, Z+W
So many times in the course of learning complex number we have to use this triangle inequality of modulus of complex number.
I believe this Triangle Inequality of Complex Number tutorial was helpful to enhance your concept in Algebra Mathematics.
If we have complex number z & w, then triangle inequality states that
(abs.Z + abs. W ) is greater than abs, Z+W
So many times in the course of learning complex number we have to use this triangle inequality of modulus of complex number.
I believe this Triangle Inequality of Complex Number tutorial was helpful to enhance your concept in Algebra Mathematics.
Prove the Triangle Inequality for Complex Numbers
The Triangle Inequalities (1 of 3: Sum of Complex Numbers)
How to Prove the Triangle Inequality for Complex Numbers
Triangle Inequality of Complex Number
Complex Analysis | Unit 1 | Lecture 10 | Triangle Inequality
Triangle Inequality for Complex Numbers
Triangle Inequalities of complex numbers|proof of triangle inequities|Complex numbers
CLASS 11 MATHS CBSE | MOST IMPORTANT QUESTIONS FOR EXAM | WITH TRICKS
Triangle Inequality / Complex Numbers
Triangle Inequality for Real Numbers Proof
TRIANGULAR INEQUALITY {COMPLEX ANALYSIS} 🔥
complex numbers triangular inequalities
JEE: Complex Numbers L6 | Triangle Inequality | Unacademy JEE | IIT JEE Maths | Sameer Chincholikar
Triangular Inequalities Complex Numbers
Triangle Inequality: proof & application (Exam Question 7 of 12)
Complex Number 04 | Triangular Inequalities Practice | Logarithm of a Complex | Class 11/JEE
Reverse Triangle Inequality -- Complex Numbers
Triangle inequality in complex number
Triangle inequality of complex numbers [Mathematical Methods I (4-2)]
Reverse triangle inequality | Properties of Modulus of Complex Numbers
Complex Number 12 | Triangular Inequality of Modulus of Complex Number | JEE/BITSAT/CET/ Class 11
Triangle Inequality: proof foundations (Exam Question 6 of 12)
Proof: Triangle Inequality Theorem | Real Analysis
Triangular inequality Proof (easy method)
Комментарии
 0:08:45
0:08:45
 0:10:46
0:10:46
 0:09:24
0:09:24
 0:05:47
0:05:47
 0:05:52
0:05:52
 0:06:55
0:06:55
 0:12:18
0:12:18
 0:05:16
0:05:16
 0:04:49
0:04:49
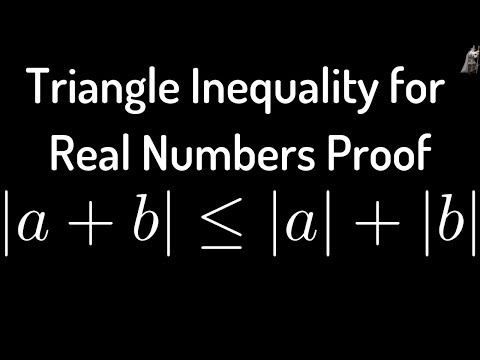 0:03:08
0:03:08
 0:07:31
0:07:31
 0:09:38
0:09:38
 1:32:44
1:32:44
 0:12:51
0:12:51
 0:12:43
0:12:43
 1:22:40
1:22:40
 0:05:01
0:05:01
 0:16:20
0:16:20
 0:33:28
0:33:28
 0:04:59
0:04:59
 0:21:22
0:21:22
 0:13:06
0:13:06
 0:05:30
0:05:30
 0:05:10
0:05:10