filmov
tv
Triangle Inequality
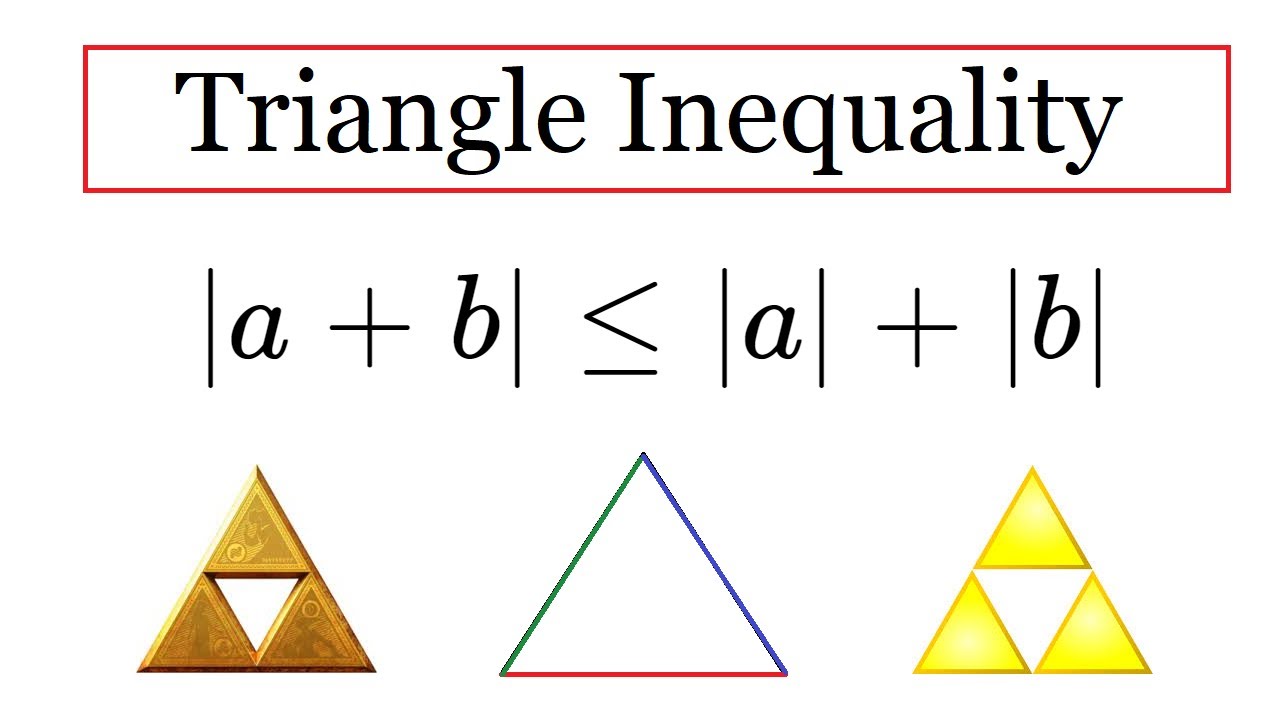
Показать описание
Triangle Inequality
In this video, I define the concept of an absolute value and use it to prove the triangle inequality in R, which is the most important inequality that we'll use in analysis. Enjoy!
In this video, I define the concept of an absolute value and use it to prove the triangle inequality in R, which is the most important inequality that we'll use in analysis. Enjoy!
Triangle inequality theorem | Perimeter, area, and volume | Geometry | Khan Academy
Triangle Inequality for Real Numbers Proof
Proof: Triangle Inequality Theorem | Real Analysis
Triangle Inequality
Triangle Inequality Theorem
Triangle Inequality Theorem Possible Values of x
Triangle Inequality Theorem - Corbettmaths
Proof: Reverse Triangle Inequality Theorem | Real Analysis
Class 16| Complete Geometry | AREA OF TRIANGLE| Shani Sharma | SSC CGL 2025
Triangle Inequality Theorem - Example | Don't Memorise
A quick proof of the triangle inequality
Triangle or Not? The Triangle Inequality Theorem
Triangle Inequality Theorem
Vector triangle inequality | Vectors and spaces | Linear Algebra | Khan Academy
Triangle inequality
The Triangle Inequalities (1 of 3: Sum of Complex Numbers)
CALCULUS. Proof Triangle Inequality (#5)
Triangle Inequality Theorem - Triangle Inequalities by @MathTeacherGon
Triangle Inequality Theorem/ The Relationships Between the Sides of a Triangle/ Geometry
Prove the Triangle Inequality for Complex Numbers
Ext2 Inequalities: The (ℝeal) Triangle Inequalities
Triangle Inequality Explained Simply
What is the Triangle Inequality Theorem - Congruent Triangles
Triangle inequality/ prep 2 geometry
Комментарии
 0:05:52
0:05:52
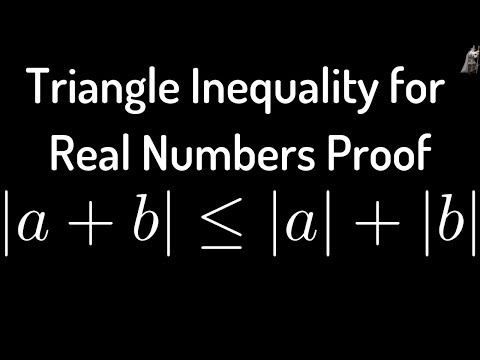 0:03:08
0:03:08
 0:05:30
0:05:30
 0:13:08
0:13:08
 0:01:01
0:01:01
 0:04:28
0:04:28
 0:08:04
0:08:04
 0:08:53
0:08:53
 1:05:19
1:05:19
 0:02:40
0:02:40
 0:00:48
0:00:48
 0:01:05
0:01:05
 0:07:25
0:07:25
 0:18:53
0:18:53
 0:00:05
0:00:05
 0:10:46
0:10:46
 0:07:27
0:07:27
 0:07:16
0:07:16
 0:04:15
0:04:15
 0:08:45
0:08:45
 0:14:01
0:14:01
 0:00:31
0:00:31
 0:06:58
0:06:58
 0:15:54
0:15:54