filmov
tv
The limit of sin(1/x) as x approaches 0 does not exist (Proof) [ILIEKMATHPHYSICS]

Показать описание
This video references "Intro to Real Analysis" by Bartle and Sherbert Fourth Edition. For more details related to the context of this video, see section 4.1. In the book, they prove this limit using the divergence criterion for limits. Here, we do so straight from the definition itself.
Thanks and enjoy the video!
Thanks and enjoy the video!
Limit of sin(1/x) as x approaches 0 Does Not Exist | Calculus 1 Exercises
The limit of sin(1/x) as x approaches 0 does not exist (Proof) [ILIEKMATHPHYSICS]
Limit of x*sin(1/x) as x approaches 0 | Calculus 1 Exercises
Limit for Trigonometric Functions sin(1/x) as x approaches zero
Oscillating Discontinuity - sin(1/x)
What is the limit of sin (1/x)? - Week 1 - Lecture 8 - Mooculus
Limit of x*sin(1/x) as x approaches Infinity | Calculus 1 Exercises
Limit of (1-x)sin(1/(1-x)) as x approaches 1 | Calculus 1 Exercises
Your Teacher LIED! This Derivative IS Easy
Limit of sin(1/x) as x approaches to zero | What is the limit of sin (1/x)?
Limits of Trigonometric Functions
Calculus Made Easy: Limits of Sine Functions at Infinity: sin(1/x) and sin(1/n^2) Explained
This is a very famous limit
lim xsin(1/x) as x goes to 0
Proving a Limit of sin(x)/x
Proofs: Lim sinx/x =1 and lim [cosx -1] /x =0 as x goes to zero from geometry
Discover the Limit of x*sin(1/x) as x Approaches Infinity | Unraveling Calculus Mysteries 🧠📈🚀...
Limit of x*sin(1/x) as x approaches infinity || Two Solutions
The Limit (do not use L'Hospital rule)
Limit of sin^(-1)(x)/x as x approaches zero using L'Hopital's Rule #shorts
limit x tend to 0 sin 1/x
Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
Limit of sin(1/x) when x approaches 0. (Urdu/Hindi)
30 Limit Approaching Infinity for Trigonometric Function xsin(1/x)
Комментарии
 0:04:36
0:04:36
 0:08:46
0:08:46
 0:08:14
0:08:14
 0:10:12
0:10:12
 0:03:20
0:03:20
 0:08:18
0:08:18
 0:09:23
0:09:23
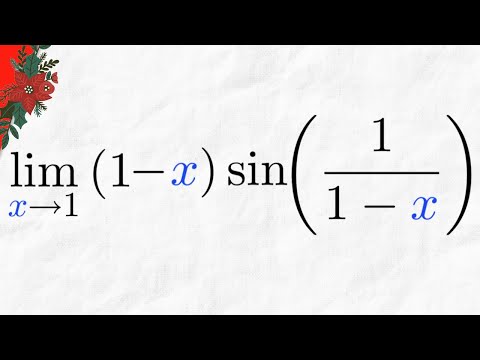 0:12:03
0:12:03
 0:06:41
0:06:41
 0:11:50
0:11:50
 0:15:23
0:15:23
 0:01:51
0:01:51
 0:00:48
0:00:48
 0:15:35
0:15:35
 0:01:00
0:01:00
 0:17:08
0:17:08
 0:03:58
0:03:58
 0:03:46
0:03:46
 0:12:08
0:12:08
 0:00:39
0:00:39
 0:02:44
0:02:44
 0:09:16
0:09:16
 0:08:47
0:08:47
 0:02:24
0:02:24