filmov
tv
Prove the Triangle Inequality for Complex Numbers
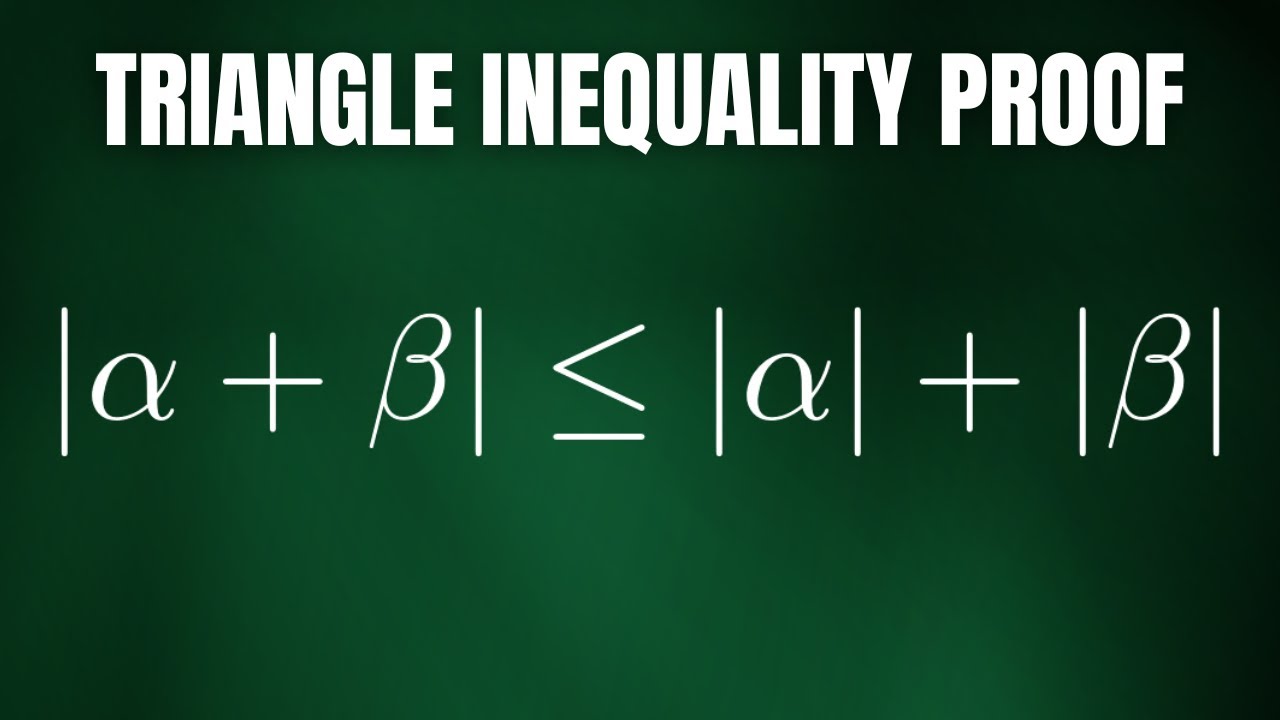
Показать описание
Prove the Triangle Inequality for Complex Numbers
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
If you enjoyed this video please consider liking, sharing, and subscribing.
There are several ways that you can help support my channel:)
************Udemy Courses(Please Use These Links If You Sign Up!)*************
Abstract Algebra Course
Advanced Calculus Course
Calculus 1 Course
Calculus 2 Course
Calculus 3 Course
Calculus 1 Lectures with Assignments and a Final Exam
Calculus Integration Insanity
Differential Equations Course
Differential Equations Lectures Course (Includes Assignments + Final Exam)
College Algebra Course
How to Write Proofs with Sets Course
How to Write Proofs with Functions Course
Trigonometry 1 Course
Trigonometry 2 Course
Statistics with StatCrunch Course
Math Graduate Programs, Applying, Advice, Motivation
Daily Devotionals for Motivation with The Math Sorcerer
Thank you:)
Triangle Inequality for Real Numbers Proof
Proof: Triangle Inequality Theorem | Real Analysis
Prove the Triangle Inequality for Complex Numbers
How to Prove the Triangle Inequality for Complex Numbers
Proof: Reverse Triangle Inequality Theorem | Real Analysis
PROVING TRIANGLE INEQUALITIES || GRADE 8 MATHEMATICS Q4
Triangle inequality theorem | Perimeter, area, and volume | Geometry | Khan Academy
CALCULUS. Proof Triangle Inequality (#5)
Approximate independence of permutation mixtures
Triangle Inequality
Proof on triangle inequalities
Reverse Triangle Inequality Absolute Value Proof
Can You Prove the Triangle Inequality?
Prove the Triangle Inequality (Real Number Case)
Triangular Inequality Proof | Real Analysis
Triangle Inequality Proof: |x+y| less than or equal to |x|+|y|
Real Analysis Course #10 - The Triangle Inequality
Triangular inequality Proof (easy method)
Triangle Inequality: proof & application (Exam Question 7 of 12)
⚠️TRIANGLE INEQUALITY PROOF in 1 MINUTE, Real numbers, Calculus inequalities, #shorts
Linear Algebra, Lesson 5, Video 16: Proof of Triangle Inequality
Proving the triangle inequality, math proofs, Learn to do mathematical proofs
The Triangle Inequality in R^n (Proof)
Vector triangle inequality | Vectors and spaces | Linear Algebra | Khan Academy
Комментарии
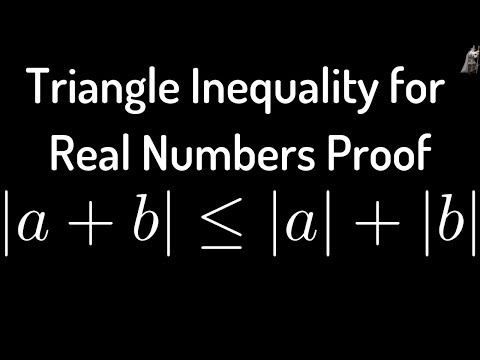 0:03:08
0:03:08
 0:05:30
0:05:30
 0:08:45
0:08:45
 0:09:24
0:09:24
 0:08:53
0:08:53
 0:30:20
0:30:20
 0:05:52
0:05:52
 0:07:27
0:07:27
 0:57:43
0:57:43
 0:13:08
0:13:08
 0:03:10
0:03:10
 0:03:37
0:03:37
 0:03:01
0:03:01
 0:14:19
0:14:19
 0:04:05
0:04:05
 0:03:11
0:03:11
 0:04:22
0:04:22
 0:05:10
0:05:10
 0:12:43
0:12:43
 0:00:59
0:00:59
 0:13:28
0:13:28
 0:04:10
0:04:10
 0:02:43
0:02:43
 0:18:53
0:18:53