filmov
tv
Solving x^6+x^4+x^2=3 | Math Olympiads
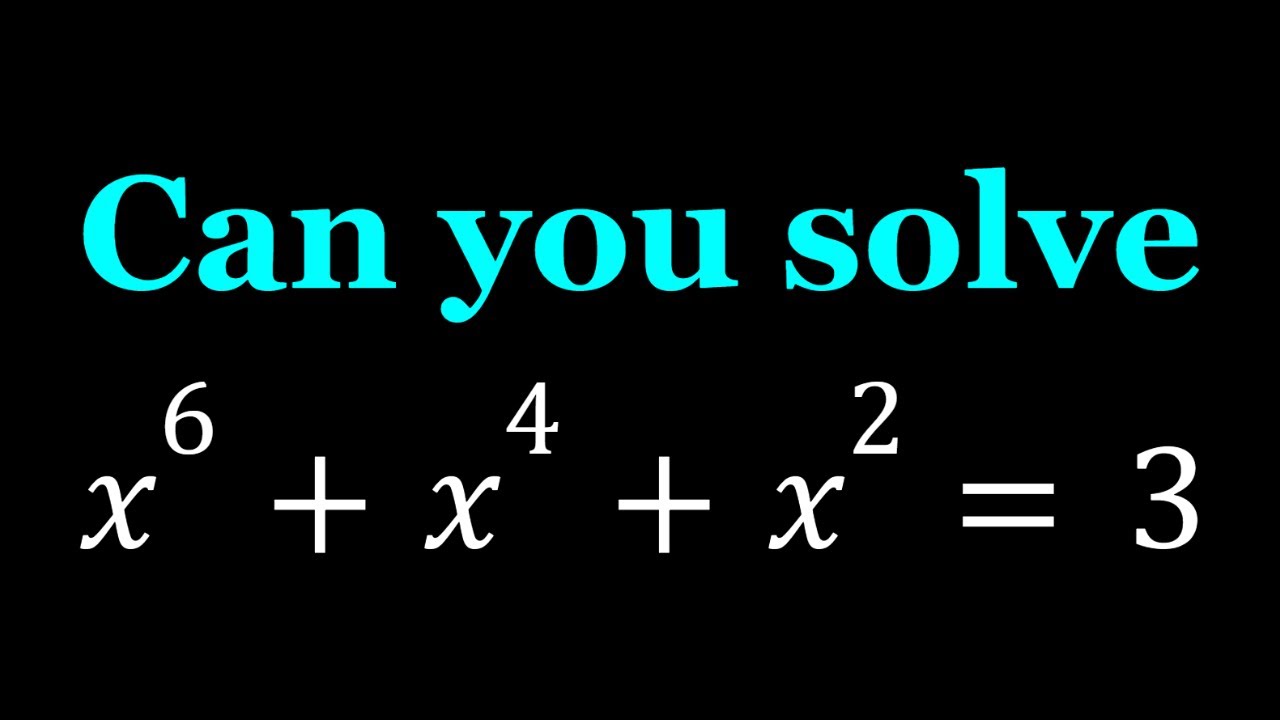
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #PolynomialEquations #Polynomials
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Solving x^6+x^4+x^2=3 | Math Olympiads
United Kingdom - A Nice Exponential Equation | Math olympiad Question
Exponential Olympiad Equation || 9^x - 6^x = 4^x ||
Solving the 2000 Korean Math Olympiad Question | Equation with Exponents | 2^x+3^x-4^x+6^x-9^x=1
How to Solve this Math Olympiad question on Algebra 9^x-6^x=4^x
Math Olympiad Question | Equation Solving | You should learn this trick
SOLVE 9^x -6^x = 4^x | MATH OLYMPIADS | A Nice Exponential Question
Norway Math Olympiad Question | You should be able to solve this!
A Nice math Olympiad simplification #olympiad #mathematics #maths #exponents #logarithm
A Nice Math Olympiad Exponential Equation 3^x = X^9
Mexico - A Nice Math Olympiad Exponential Problem
Olympiad Math Question | How To Solve 6th Degree Polynomial Equations | x^6–x^3=2
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
A Nice Olympiad Exponential Multiplication Problem #short #olympiad #mathematics #maths #exponents
Russia | Math Olympiad Question | You should know this trick!!
Factor: x^4 + x^3 - 4x^2 + x +1 | Olympiad Question
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
Nice Olympiad Math | x^2–x^3=12 | Nice Math Olympiad Solution
Mathematical Olympiad | Learn how to solve exponential equation quickly | Math Olympiad Training
Mathematical Olympiad | Solve for a+b | Math Olympiad Preparation
A Nice Olympiad Math Problem X^2x^6=3 | Quick Trick!!!
Olympiad Question | Solve the Radical Equation with Rational exponents | Math Olympiad Training
South Africa Math Olympiad Question
Math Olympiad challenge 36^x+6^x=2 | Quick Trick!!!
Комментарии
 0:12:17
0:12:17
 0:09:19
0:09:19
 0:10:06
0:10:06
 0:06:19
0:06:19
 0:08:16
0:08:16
 0:05:30
0:05:30
 0:06:39
0:06:39
 0:03:21
0:03:21
 0:00:51
0:00:51
 0:02:34
0:02:34
 0:08:36
0:08:36
 0:25:59
0:25:59
 0:10:49
0:10:49
 0:00:52
0:00:52
 0:08:01
0:08:01
 0:09:34
0:09:34
 0:01:54
0:01:54
 0:15:05
0:15:05
 0:04:38
0:04:38
 0:08:59
0:08:59
 0:05:58
0:05:58
 0:08:03
0:08:03
 0:06:45
0:06:45
 0:08:17
0:08:17