filmov
tv
Russia | Math Olympiad Question | You should know this trick!!

Показать описание
Math Olympiad Problem
Russia | Math Olympiad Question | You should know this trick!!
Russian Math Olympiad Question
Russian Math Olympiad | A Very Nice Geometry Problem
Solve for positive integer solutions| Math Olympiad #maths #matholympiad
Russian Math Olympiad Question || Find the value of X ||
Russian Math Olympiad Question
Russian -Math Olympiad|Solve for x and y#math #matholympiad
Russia - Math Olympiad Question. A Nice Radical Math Problem.
Russia| Moscow Math Olympiad Question from 1995 | Geendle
Russia | Math Olympiad Question | 90% Failed to solve!
Russia Math Olympiad Question | You Should Know This
Russian Math Olympiad Question | Nice Exponent Math Simplification Problem
Can you solve? A nice math problem to solve #maths #mathematics
How to solve this Russian Olympiad Math Questions | Learn the trick to solve this Math Problem
World champion in mental calculation 🏆
Russia Math Olympiad Question || You should learn this trick!
Russian Math Olympiad Question
Russia | Math Olympiad Question | Can You Solve it?
Russia Math Olympiad Question You should know this trick!!
Russian Math Olympiad Question
Russian | You should know this | Math Olympiad Trick
Russian Math Olympiad - Math Contest
A Nice Math Olympiad Exponential Equation 3^x = X^9
Luxembourg - Math Olympiad Question | You should know this trick
Комментарии
 0:08:01
0:08:01
 0:03:42
0:03:42
 0:14:34
0:14:34
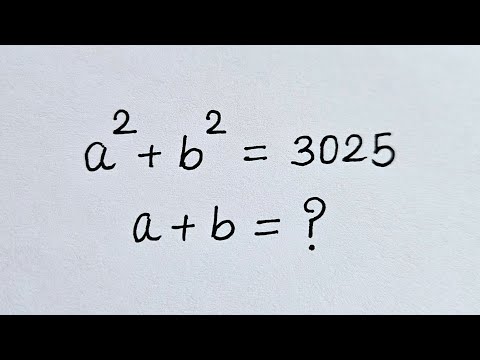 0:09:49
0:09:49
 0:03:42
0:03:42
 0:02:35
0:02:35
 0:10:40
0:10:40
 0:02:30
0:02:30
 0:06:17
0:06:17
 0:16:40
0:16:40
 0:05:17
0:05:17
 0:02:01
0:02:01
 0:05:24
0:05:24
 0:09:35
0:09:35
 0:00:24
0:00:24
 0:10:59
0:10:59
 0:07:04
0:07:04
 0:03:28
0:03:28
 0:11:22
0:11:22
 0:03:51
0:03:51
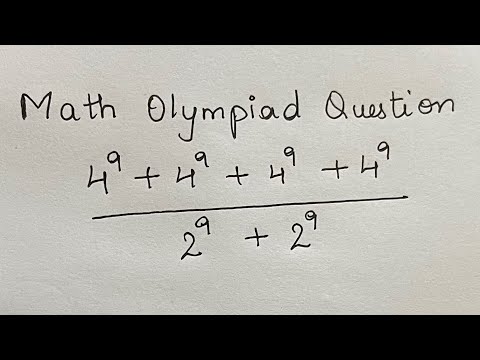 0:01:26
0:01:26
 0:03:57
0:03:57
 0:02:34
0:02:34
 0:02:51
0:02:51