filmov
tv
Math Olympiad Question | Equation Solving | You should learn this trick

Показать описание
How to solve this equation? By using this trick, you can deal it quickly!
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
A Good Math Olympiad Algebra Equation | Math Olympiad Questions | Beautiful Exponential Equation
Math Olympiad Question | Equation Solving | You should learn this trick
Math Olympiad Question | Algebra Equation Solving | You should be able to solve this!!
Thailand | Math Olympiad Question | Nice Algebra Equation
Can you solve the equation? | (Mathematical Olympiad Training) | #math #maths
Math Olympiad Question | Nice Algebra Equation | You should know this trick!!
A Nice Math Olympiad Exponential Equation X^4 = 2^x
Math Olympiad Question | Equation Solving | You should use this trick
United Kingdom - A Nice Exponential Equation | Math olympiad Question
A beautiful international math olympiad problem
Kosovo - Math Olympiad Question | A Nice Algebraic Equation
Math Olympiad Question | You should know this trick!!
A Nice Math Olympiad Exponential Equation 3^x = X^9
Math Olympiad 3^m–2^m=65 | Math Olympiad Problems | Algebra
Olympiad Question | Solve the Radical Equation with Cube and Square Roots | Math Olympiad Training
Norway Math Olympiad Question | You should be able to solve this!
Germany | A nice Logarithmic Math Olympiad Problem | Exponential Equation x^log27+3^logx=36 | x=?
Solving the hardest question of a British Mathematical Olympiad
France - Math Olympiad Question | An Algebraic Expression | You should be able to solve this!
Math Olympiad Practice
Hardest Exam Question | Only 8% of students got this math question correct
A nice math Olympiad question #math #matholympiad
South Africa Math Olympiad Question
Комментарии
 0:01:54
0:01:54
 0:11:13
0:11:13
 0:05:30
0:05:30
 0:09:15
0:09:15
 0:01:26
0:01:26
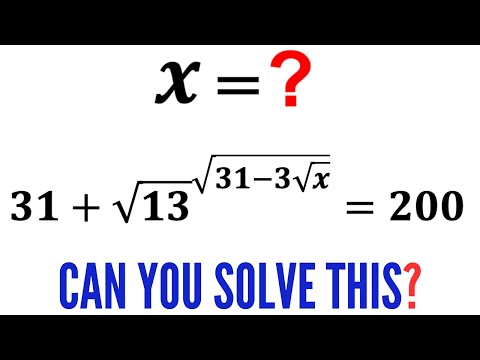 0:04:47
0:04:47
 0:07:26
0:07:26
 0:03:18
0:03:18
 0:05:10
0:05:10
 0:09:19
0:09:19
 0:01:00
0:01:00
 0:03:01
0:03:01
 0:00:33
0:00:33
 0:02:34
0:02:34
 0:10:49
0:10:49
 0:08:11
0:08:11
 0:03:21
0:03:21
 0:12:15
0:12:15
 0:11:26
0:11:26
 0:08:40
0:08:40
 0:01:00
0:01:00
 0:11:28
0:11:28
 0:07:53
0:07:53
 0:06:45
0:06:45