filmov
tv
South Africa Math Olympiad Question
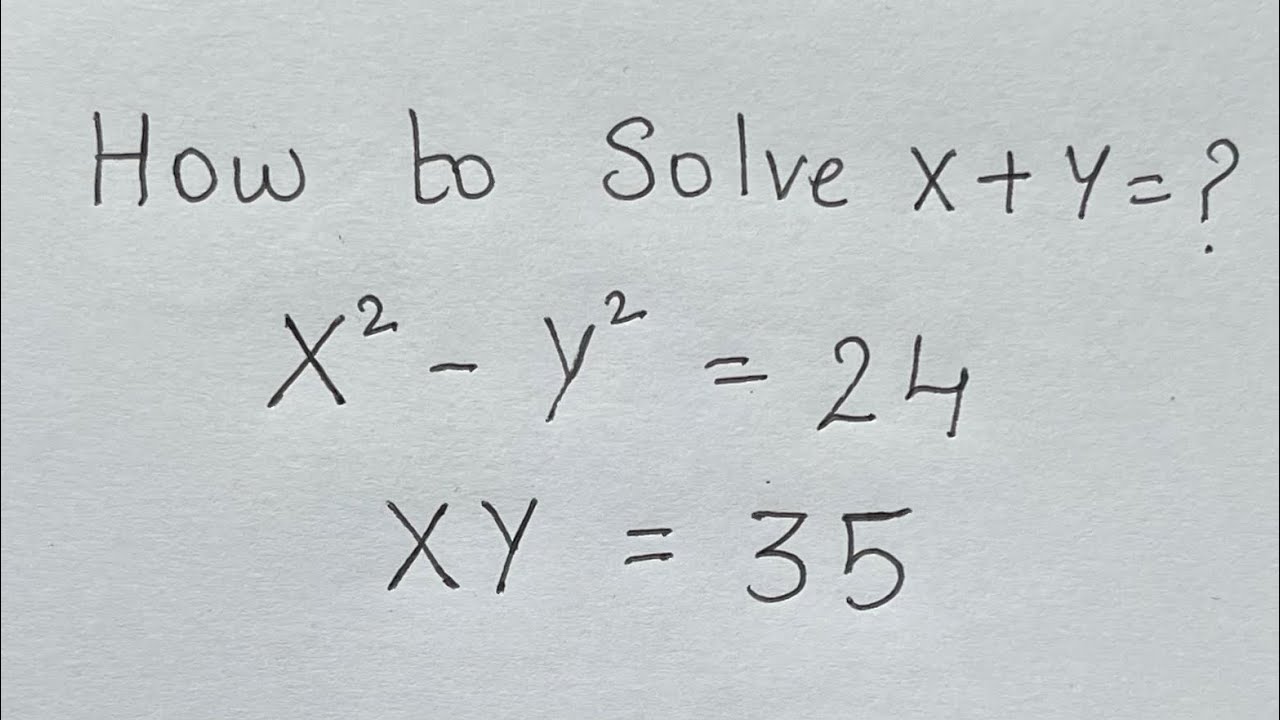
Показать описание
Maths Olympiads are held all around the world to recognise students who excel in maths. The test is offered at many grade levels and provides them with numerous possibilities to win certifications, awards, and even scholarships for higher studies
South Africa Math Olympiad Question
South Africa Math Olympiad Question
South Africa math olympiad question | You should be able to do this !!!
South Africa | Mathematical Olympiad Question
South African Math Olympiad - An Interesting System of Equations
South Africa Math || Olympiad Question
South Africa Math Olympiad Question
How to Efficiently Solve This South Africa Math Olympiad Question | Two Methods
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam
South Africa Math Olympiad Question ✍️ Find the Value of X ✍️
A Nice Math Olympiad Exponential Equation 3^x = X^9
South Africa Math Olympiad Question ✍️ Find the Value of X ✍️
South Africa Maths Olympiad Question #matholympiad #exponents
South Africa 🇿🇦 Math Olympiad Question | Find the value of x+y=? | Check yourself 🧠
South Africa Math Olympiad Question
EKSE: South African Mathematics Foundation Ahead of Pan African Mathematics Olympiad
South Africa Math Olympiad Question
South Africa Math Olympiad Question | Simultaneous Equation | You Should Know This Trick
Young lady absolutely kills it in Nigerian Maths Competition!
South Africa 🇿🇦 Math Olympiad Question | Check yourself 🧠
South Africa | Can you solve this ? | A nice olympiad algebra problem.
South Africa 🇿🇦 Math Olympiad Question | Find the value of x=? | Check yourself 🧠
Luxembourg - Math Olympiad Question | You should know this trick
South African Maths Olympiad Question | Equation Based | you should learn easily | find x and y
Комментарии
 0:06:45
0:06:45
 0:11:03
0:11:03
 0:02:09
0:02:09
 0:03:26
0:03:26
 0:05:33
0:05:33
 0:08:24
0:08:24
 0:00:36
0:00:36
 0:13:26
0:13:26
 0:01:54
0:01:54
 0:10:05
0:10:05
 0:02:34
0:02:34
 0:09:26
0:09:26
 0:03:06
0:03:06
 0:09:09
0:09:09
 0:01:09
0:01:09
 0:06:33
0:06:33
 0:01:33
0:01:33
 0:09:45
0:09:45
 0:01:35
0:01:35
 0:07:17
0:07:17
 0:06:49
0:06:49
 0:04:32
0:04:32
 0:02:51
0:02:51
 0:12:13
0:12:13