filmov
tv
Math Olympiad Question | Equation solving | You should learn this trick to pass the exam

Показать описание
Equation solving with best tricks ever and excell in exams!
Thanks for watching and always supporting!
Maths Olympiad is an examination curated with advanced level mathematics to work on a student's current potential. In such tests, the students are required to solve the given questions. Based on the problem solving, the student is rewarded with marks and accolades. To support this we provide with solutions for the toughest and all level of questions.
We offer an ample amount of Math Olympiad Problems for the student to be ready and practice their way to perfection. We also provide the international level of maths Olympiad questions on this channel.
Benefits of Math Olympiad
* Fantastic exposure to the level of complicated mathematics.
* Great opportunity to test you whether one is ready for the said complicated mathematics.
* If someone is passionate about mathematics, Olympiads will undoubtedly be an extraordinary chance to stay in touch with your passion.
* Olympiads can also be an excellent way to prepare for the future if someone is looking ahead to take up mathematics for their higher studies.
* Olympiads give a chance to get acquainted with your weaknesses and strengths and work on them.
* Since Olympiads happen quite a few times, around the year, this can help keep those skills under practice.
Thanks for watching and always supporting!
Maths Olympiad is an examination curated with advanced level mathematics to work on a student's current potential. In such tests, the students are required to solve the given questions. Based on the problem solving, the student is rewarded with marks and accolades. To support this we provide with solutions for the toughest and all level of questions.
We offer an ample amount of Math Olympiad Problems for the student to be ready and practice their way to perfection. We also provide the international level of maths Olympiad questions on this channel.
Benefits of Math Olympiad
* Fantastic exposure to the level of complicated mathematics.
* Great opportunity to test you whether one is ready for the said complicated mathematics.
* If someone is passionate about mathematics, Olympiads will undoubtedly be an extraordinary chance to stay in touch with your passion.
* Olympiads can also be an excellent way to prepare for the future if someone is looking ahead to take up mathematics for their higher studies.
* Olympiads give a chance to get acquainted with your weaknesses and strengths and work on them.
* Since Olympiads happen quite a few times, around the year, this can help keep those skills under practice.
Комментарии
 0:00:33
0:00:33
 0:03:01
0:03:01
 0:09:15
0:09:15
 0:02:44
0:02:44
 0:07:54
0:07:54
 0:11:43
0:11:43
 0:01:54
0:01:54
 0:07:59
0:07:59
 0:00:52
0:00:52
 0:04:51
0:04:51
 0:06:37
0:06:37
 0:08:47
0:08:47
 0:00:37
0:00:37
 0:11:01
0:11:01
 0:00:48
0:00:48
 0:00:28
0:00:28
 0:00:29
0:00:29
 0:08:23
0:08:23
 0:00:48
0:00:48
 0:00:22
0:00:22
 0:00:49
0:00:49
 0:05:30
0:05:30
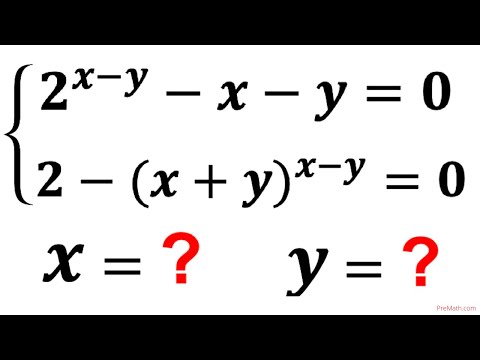 0:10:15
0:10:15
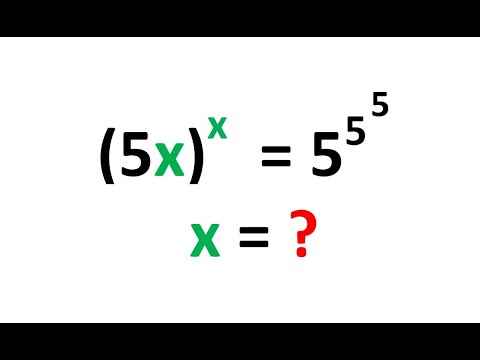 0:05:07
0:05:07