filmov
tv
Factor: x^4 + x^3 - 4x^2 + x +1 | Olympiad Question
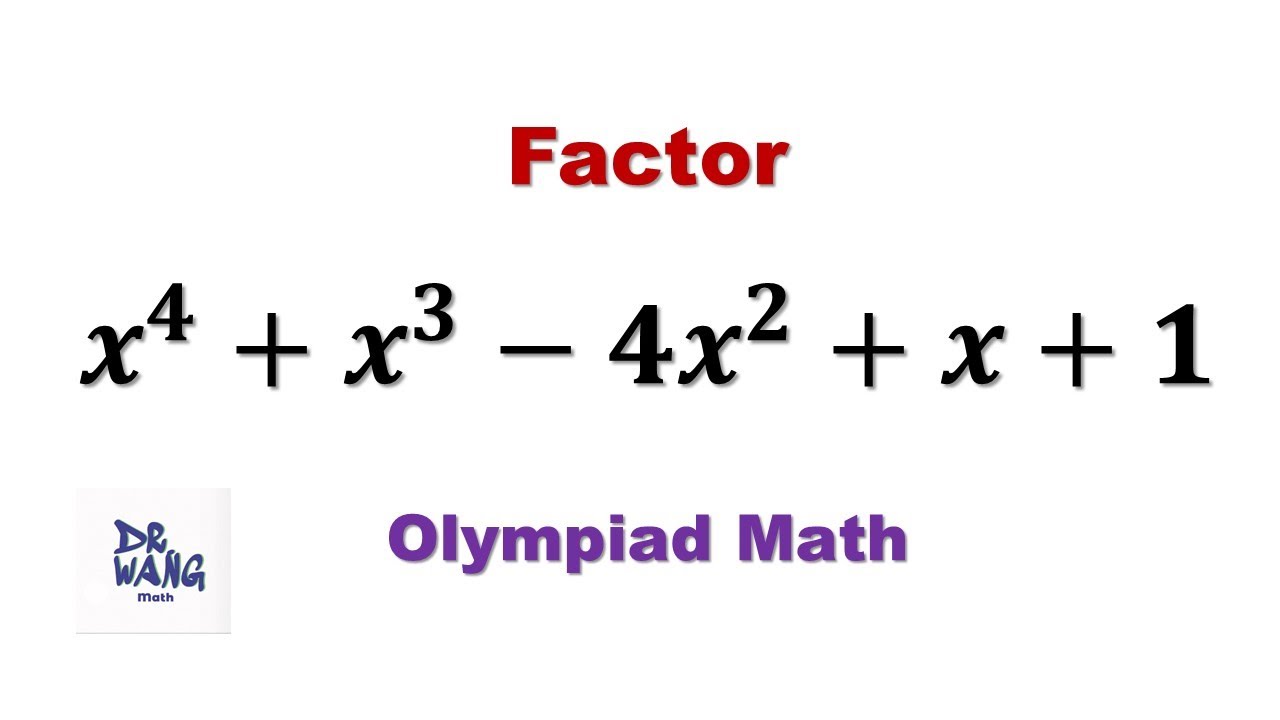
Показать описание
We introduce two methods to solve this problem. First, we find a root using the formula for the relationship of the roots to the polynomial coefficients, and then factorize using long division. Repeating the same idea, we got the answer. The second method is unusual. The idea is based on the completing the square method.
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
Factoring a polynomial to the fourth power using factoring to second power
Factoring a quintic x^5+x^4+x^3+x^2+x+1 by grouping
Factor: x^4 + x^3 - 4x^2 + x +1 | Olympiad Question
Factoring 5-term polynomials by grouping
How to factorise x^4+4x^2+3 || Factor x4+4x2+3 || bi-quadratic polynomial
Factoring Trinomials
Factorise x^2+4x+3 | Factor x2+4x+3
YOU DON'T HAVE TO SAY YOU LOVE ME(DUSTY SPRINGFIELD) AMERICAN'S GOT TALENT TRENDING AUDITI...
x^3 - 3x^2 + 4x - 12 factor completely.
Factoring a third degree polynomial with four terms by grouping
4x^4 - 8x^3 -3x^2 +5x +2 = 0 Steps to Solve Quartic Polynomial Equation
Solving Polynomial Equations By Factoring and Using Synthetic Division
Solving x^2 + 4x + 3 = 0 by Factoring
FAZLIDDIN ABDUVOHIDOV BELALIM / HAMMANI YIG'LATDI / MUNISA QANDAY YORDAM BERDI? 😱 X FAKTOR БЕЛА...
How to factor x^3-64 vs x^3-64x
Factorize x⁴ + 3x² + 4
Factorising cubic functions: The kx method
Factoring Difference of Cubes x^3 - 8
FASTEST way to factor a trinomial! #shorts
How To Factor Polynomials The Easy Way!
Solving Quadratic Equations by Factoring│Algebra
How to determine if a factor is a factor of a polynomial using factor theorem
Factorize x³+x²-4x-4 by using factor theorem
Комментарии
 0:04:55
0:04:55
 0:03:26
0:03:26
 0:02:36
0:02:36
 0:09:34
0:09:34
 0:05:33
0:05:33
 0:02:23
0:02:23
 0:04:17
0:04:17
 0:01:36
0:01:36
 0:03:05
0:03:05
 0:00:31
0:00:31
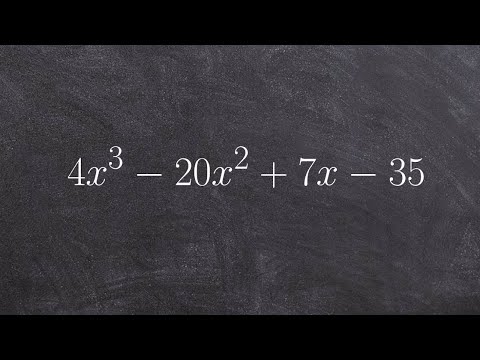 0:02:16
0:02:16
 0:11:52
0:11:52
 0:14:19
0:14:19
 0:01:34
0:01:34
 0:02:49
0:02:49
 0:04:59
0:04:59
 0:03:20
0:03:20
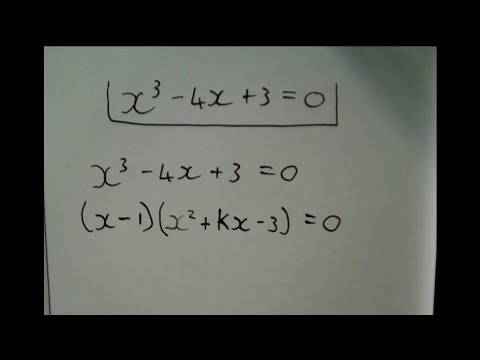 0:10:22
0:10:22
 0:01:19
0:01:19
 0:00:55
0:00:55
 0:11:54
0:11:54
 0:22:30
0:22:30
 0:02:56
0:02:56
 0:04:12
0:04:12