filmov
tv
Solving a Quartic Equation
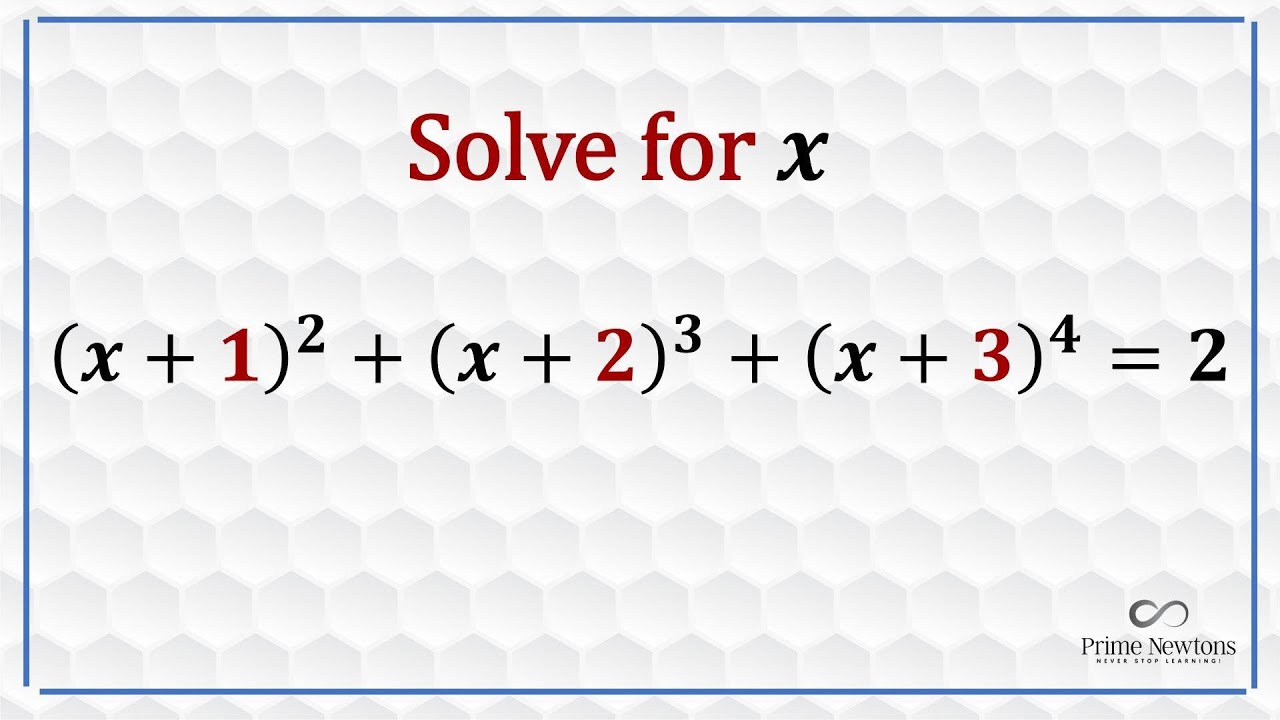
Показать описание
You should not take calculus if you can't solve this. This video utilizes the most common strategies adopted in solving calculus problems. I used substitution, factoring, theorems, synthetic division and the quadratic formula
Solving a Quartic Equation
Solving a Quartic Equation with Quadratic Techniques
How To Solve The Quartic Equation?
The most fun way of solving this quartic equation
Solving a Quartic Equation
How to solve quartic equations. Easy process - Mathsomniac
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
Solving a quartic equation using an unusual idea. An algebraic challenge.
How To Solve Quadratic Equations Using The Quadratic Formula
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
HOW TO SOLVE QUARTIC EQUATION || HOW TO SOLVE FOURTH DEGREE EQUATION || QUARTIC EQUATION PROBLEM
A quartic equation solved in two ways! No quartic formula!!! x^4+4x-1=0
How to Solve Quartic Equation in Quadratic Form
Solving general quartic equations
solving equations but they get increasingly awesome
Solving a quartic equation with parameters
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
01 - Solving Equations in Quadratic Form - Part 1 (Learn to Solve Equations in Algebra)
How to solve the quartic equation by the Ferrari method?
Quadratic Equations | Solve by factoring | Free Math Videos
500 years of NOT teaching THE CUBIC FORMULA. What is it they think you can't handle?
Solving Polynomial Equations By Factoring and Using Synthetic Division
[Algebra] Derive the quartic formula
Комментарии
 0:17:08
0:17:08
 0:06:57
0:06:57
 0:10:05
0:10:05
 0:06:39
0:06:39
 0:10:13
0:10:13
 0:09:30
0:09:30
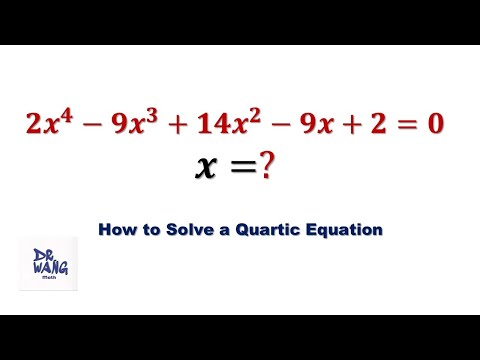 0:06:21
0:06:21
 0:17:05
0:17:05
 0:05:56
0:05:56
 0:04:55
0:04:55
 0:12:29
0:12:29
 0:04:42
0:04:42
 0:14:36
0:14:36
 0:02:33
0:02:33
 0:35:34
0:35:34
 0:10:44
0:10:44
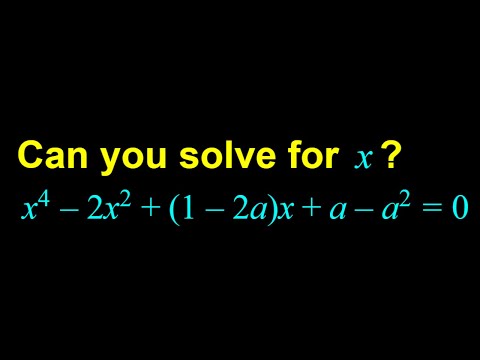 0:11:26
0:11:26
 0:00:30
0:00:30
 0:37:08
0:37:08
 0:13:19
0:13:19
 0:02:43
0:02:43
 0:36:58
0:36:58
 0:14:19
0:14:19
![[Algebra] Derive the](https://i.ytimg.com/vi/vsa05oa06Ck/hqdefault.jpg) 0:44:45
0:44:45