filmov
tv
Solving a quartic equation using an unusual idea. An algebraic challenge.

Показать описание
This video is about a quartic equation that can be solved without the formula. Two methods shown.
Polynomial expressions,difference of squares,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,Polynomial equations,an algebraic challenge,quartic equations,How to factor a quartic using an unusual method,A quartic equation that can be solved without the formula.
Polynomial expressions,difference of squares,algebra,algebraic equations,SyberMath,algebraic manipulations,equations,substitution,Challenging Math Problems,Non-routine Math Problems,polynomial equations,an algebra challenge,algebraic identities,non-standard methods,symmetry,math,maths,mathematics,Polynomial equations,an algebraic challenge,quartic equations,How to factor a quartic using an unusual method,A quartic equation that can be solved without the formula.
Solving a Quartic Equation with Quadratic Techniques
How To Solve Quadratic Equations Using The Quadratic Formula
The most fun way of solving this quartic equation
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
Solving a Quartic Equation
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
Solving a quartic equation using an unusual idea. An algebraic challenge.
How to solve quartic equations. Easy process - Mathsomniac
A Nice Radical Equation | Using The Factorisation Method.
How To Solve The Quartic Equation?
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
Solving Quadratic Equations using Quadratic Formula - Quadratic Equations
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
How to Solve Quadratic Equations - Using 3 Different Methods
Quadratic Equations | Solve by factoring | Free Math Videos
solving equations but they get increasingly awesome
Solving Polynomial Equations By Factoring and Using Synthetic Division
How to solve the quartic equation by the Ferrari method?
Solving an equation by quadratic formula
Solving using the quadratic formula with complex solutions
4 WAYS TO SOLVE A QUADRATIC EQUATION | Algebra 1 & 2 | Factoring, Square Roots, Quadratic Formul...
Solving a quartic equation with parameters
Quadratic Equations Grade 10
01 - Solving Equations in Quadratic Form - Part 1 (Learn to Solve Equations in Algebra)
Комментарии
 0:06:57
0:06:57
 0:05:56
0:05:56
 0:06:39
0:06:39
 0:04:55
0:04:55
 0:17:08
0:17:08
 0:12:29
0:12:29
 0:17:05
0:17:05
 0:09:30
0:09:30
 0:06:12
0:06:12
 0:10:05
0:10:05
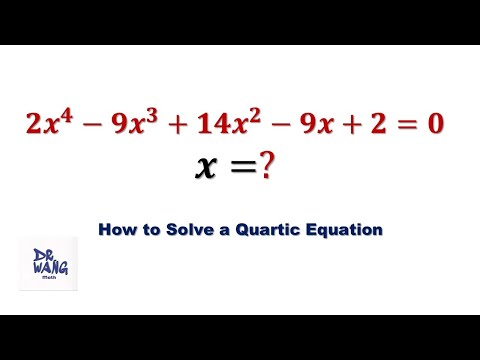 0:06:21
0:06:21
 0:09:06
0:09:06
 0:00:30
0:00:30
 0:09:30
0:09:30
 0:02:43
0:02:43
 0:10:44
0:10:44
 0:14:19
0:14:19
 0:13:19
0:13:19
 0:04:13
0:04:13
 0:05:28
0:05:28
 0:08:20
0:08:20
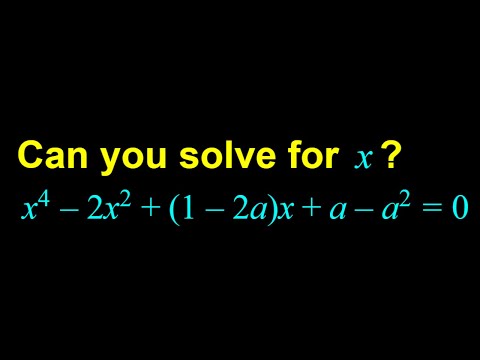 0:11:26
0:11:26
 0:05:17
0:05:17
 0:37:08
0:37:08