filmov
tv
Solving a quartic equation with parameters

Показать описание
This video is about an equation with a parameter. Two methods are shown.
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FactoringPolynomials
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #FactoringPolynomials
Solving a Quartic Equation with Quadratic Techniques
Solving a Quartic Equation
How To Solve The Quartic Equation?
The most fun way of solving this quartic equation
Solving a quartic equation using an unusual idea. An algebraic challenge.
How to factor a hard 4th degree polynomial (no rational zero, can't do it by grouping)
A quartic equation, how to solve it? A special way makes it easy | Olympiad Math Practice
Solving a Quartic Equation
imo algebra | A Nice Algebra Problem | math olympiad | 😭😭👇YouTube KKC Chandan #math #trending...
solving equations but they get increasingly awesome
How to solve quartic equations. Easy process - Mathsomniac
Solving a quartic equation with parameters
Quadratic Equation Shortcut Trick | Solve Equation in 5 Seconds
Solution of the Quartic Equation
How To Solve Quadratic Equations By Factoring - Quick & Simple! | Algebra Online Course
How To Solve Quadratic Equations Using The Quadratic Formula
How to solve the quartic equation by the Ferrari method?
HOW TO SOLVE QUARTIC EQUATION || HOW TO SOLVE FOURTH DEGREE EQUATION || QUARTIC EQUATION PROBLEM
Quadratic Equations | Solve by factoring | Free Math Videos
Solving A Quartic Equation | x⁴+12x+3=0
4 WAYS TO SOLVE A QUADRATIC EQUATION | Algebra 1 & 2 | Factoring, Square Roots, Quadratic Formul...
The Better Quadratic Formula You Won't Be Taught
01 - Solving Equations in Quadratic Form - Part 1 (Learn to Solve Equations in Algebra)
A quartic equation that can be solved easily. No quartic formula needed.
Комментарии
 0:06:57
0:06:57
 0:17:08
0:17:08
 0:10:05
0:10:05
 0:06:39
0:06:39
 0:17:05
0:17:05
 0:04:55
0:04:55
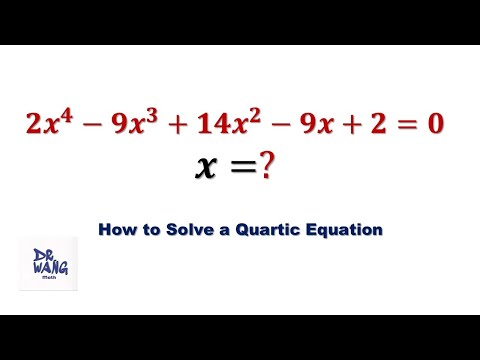 0:06:21
0:06:21
 0:10:13
0:10:13
 0:16:09
0:16:09
 0:10:44
0:10:44
 0:09:30
0:09:30
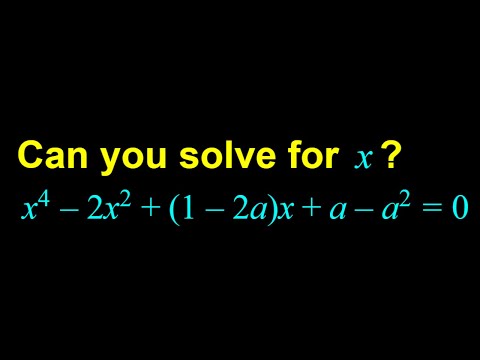 0:11:26
0:11:26
 0:00:30
0:00:30
 0:01:22
0:01:22
 0:12:29
0:12:29
 0:05:56
0:05:56
 0:13:19
0:13:19
 0:04:42
0:04:42
 0:02:43
0:02:43
 0:09:15
0:09:15
 0:08:20
0:08:20
 0:03:02
0:03:02
 0:37:08
0:37:08
 0:05:52
0:05:52