filmov
tv
Proof of a Characterization of Cut Vertices | Graph Theory

Показать описание
A vertex v, of a connected graph G, is a cut vertex if and only if there exist two vertices u and w - distinct from v - such that every u-w path in G contains v. We'll be proving this characterization of cut vertices in today's video graph theory lesson!
The second direction is to assume that v is a vertex of G that lies on every u-w path for two vertices u and w, neither equal to v in G. Then we show v must be a cut vertex of G by analyzing the graph G-v, which clearly cannot have a u-w path. Thus G-v must be disconnected, so v is a cut vertex.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
+WRATH OF MATH+
Follow Wrath of Math on...
The second direction is to assume that v is a vertex of G that lies on every u-w path for two vertices u and w, neither equal to v in G. Then we show v must be a cut vertex of G by analyzing the graph G-v, which clearly cannot have a u-w path. Thus G-v must be disconnected, so v is a cut vertex.
I hope you find this video helpful, and be sure to ask any questions down in the comments!
+WRATH OF MATH+
Follow Wrath of Math on...
Real Analysis 47 | Proof of Taylor's Theorem
Characterization of convex functions - Proof of Theorem 5.1
Proof: Supremum of {n/(n+1)} = 1 | Real Analysis
Proof: f(x) = |x| is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof: Archimedean Principle of Real Numbers | Real Analysis
Proof of Taylor's Theorem from Real Analysis
Proof of a Limit Value Using Epsilon and Delta
Proof: Reverse Triangle Inequality Theorem | Real Analysis
Proof 1 - Variance - Doughterty Review Chapter-Econometrics
The Bolzano–Weierstrass theorem, a proof from real analysis
Proof: The Limit of a Sequence is Unique | Real Analysis
Citing evidence in literary analysis | Reading | Khan Academy
Epsilon Proof for Equal Real Numbers | Real Analysis
Real Analysis 56 | Proof of the Fundamental Theorem of Calculus
Proof: Triangle Inequality Theorem | Real Analysis
Triangle Inequality for Real Numbers Proof
Proof: Supremum and Infimum are Unique | Real Analysis
Proof: Sequence (-1)^n Diverges | Real Analysis
Complex Analysis: Residue Theorem Proof
Proof: Sequence (3n+1)/(n+2) Converges to 3 | Real Analysis
Proof: e^x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Proof: A Useful Absolute Value Inequality | Real Analysis
Proof: Convergent Sequence is Bounded | Real Analysis
Proof: f(x) = x is Continuous using Epsilon Delta Definition | Real Analysis Exercises
Комментарии
 0:10:56
0:10:56
 0:15:08
0:15:08
 0:10:20
0:10:20
 0:04:19
0:04:19
 0:06:26
0:06:26
 0:15:04
0:15:04
 0:09:17
0:09:17
 0:08:53
0:08:53
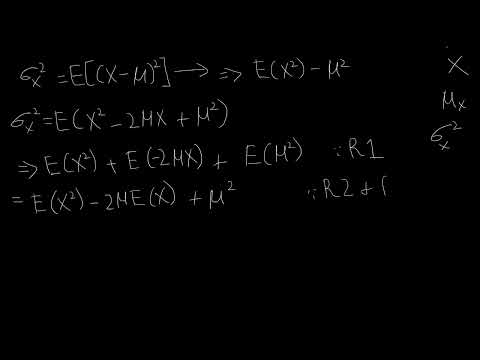 0:04:26
0:04:26
 0:13:30
0:13:30
 0:13:22
0:13:22
 0:05:20
0:05:20
 0:04:07
0:04:07
 0:12:18
0:12:18
 0:05:30
0:05:30
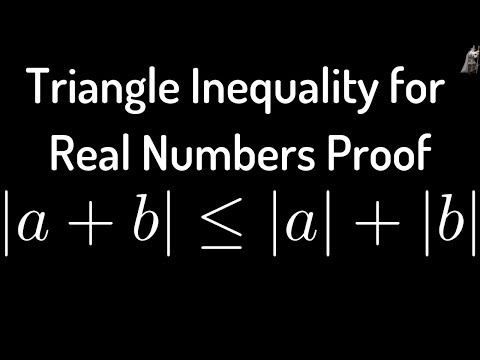 0:03:08
0:03:08
 0:04:21
0:04:21
 0:13:07
0:13:07
 0:14:53
0:14:53
 0:06:53
0:06:53
 0:14:36
0:14:36
 0:07:45
0:07:45
 0:05:47
0:05:47
 0:04:46
0:04:46